在平面直角坐标系xOy中，对于点P（x，y），以及两个无公共点的图形W1和W2，若在图形W1和W2上分别存在点M（x1，y1）和N（x2，y2），使得P是线段MN的中点，则称点M和N被点P“关联”，并称

Question

在平面直角坐标系 xOy中，对于点P（x，y），以及两个无公共点的图形W₁和W₂，若在图形W₁和W₂上分别存在点M （x₁，y₁ ）和N （x₂，y₂ ），使得P是线段MN的中点，则称点M 和N被点P“关联”，并称点P为图形W₁和W₂的一个“中位点”，此时P，M，N三个点的坐标满足x= (x1+x2)/(2)，y= (y1+y2)/(2)

（1）已知点A（0，1），B（4，1），C（3，-1），D（3，-2），连接AB，CD．
①对于线段AB和线段CD，若点A和C被点P“关联”，则点P的坐标为___；
②线段AB和线段CD的一“中位点”是Q （2，- (1)/(2)），求这两条线段上被点Q“关联”的两个点的坐标；
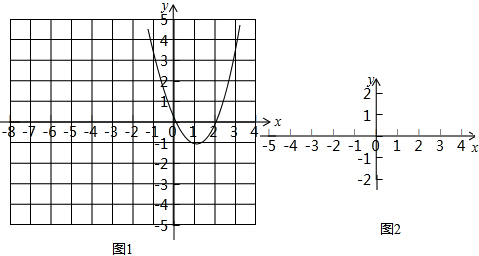
（2）如图1，已知点R（-2，0）和抛物线W₁：y=x²-2x，对于抛物线W₁上的每一个点M，在抛物线W₂上都存在点N，使得点N和M 被点R“关联”，请在图1 中画出符合条件的抛物线W₂；
（3）正方形EFGH的顶点分别是E（-4，1），F（-4，-1），G（-2，-1），H（-2，1）， T的圆心为T（3，0），半径为1．请在图2中画出由正方形EFGH和 T的所有“中位点”组成的图形（若涉及平面中某个区域时可以用阴影表示），并直接写出该图形的面积．

Answer 1

（1）①∵点A和C被点P“关联”，
又∵(0+3)/(2)=(3)/(2)，(1-1)/(2)=0，
∴点P坐标（(3)/(2)，0），
故答案为（(3)/(2)，0）．
②设在线段AB和线段CD上分别存在K（x，1）和L（3，y）被点Q（2，-(1)/(2)）“关联”，则点Q是KL中点，
∴2=(x+3)/(2)，-(1)/(2)=(1+y)/(2)，
∴x=1，y=-2，
∴这两条线段上被点Q“关联”的两个点的坐标分别是（1，1）和（3，-2）．
（2）所求作的抛物线如图1所示，

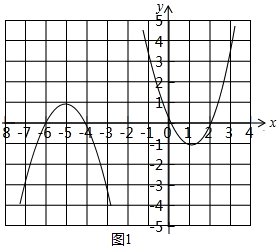
（3）正方形EFGH和 T的所有“中位点”组成的图形如图2所示（影阴部分包括边界），

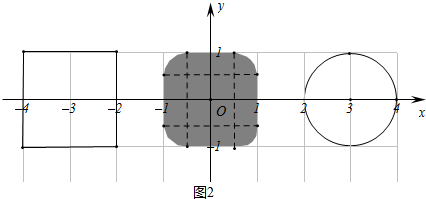
S_阴=2×2-4[(1)/(2)×(1)/(2)-(1)/(4)•π•（(1)/(2)）²]=3+(π)/(4)．