早教吧作业答案频道 -->数学-->
阅读下面材料:如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2=kx交于A(1,3)和B(-3,-1)两点.观察图象可知:①当x=-3或1时,y1=y2;②当-3<x<0或x>1时,y1&g
题目详情
阅读下面材料:
如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2=
交于A(1,3)和B(-3,-1)两点.
观察图象可知:
①当x=-3或1时,y1=y2;
②当-3<x<0或x>1时,y1>y2,即通过观察函数的图象,可以得到不等式ax+b>
的解集.
有这样一个问题:求不等式x3+4x2-x-4>0的解集.
某同学根据学习以上知识的经验,对求不等式x3+4x2-x-4>0的解集进行了探究.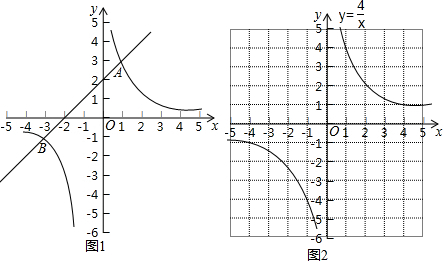
下面是他的探究过程,请将(2)、(3)、(4)补充完整:
(1)将不等式按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,原不等式可以转化为x2+4x-1>
;
当x<0时,原不等式可以转化为x2+4x-1<
;
(2)构造函数,画出图象
设y3=x2+4x-1,y4=
,在同一坐标系中分别画出这两个函数的图象.
双曲线y4=
如图2所示,请在此坐标系中画出抛物线y3=x2+4x-1;(不用列表)
(3)确定两个函数图象公共点的横坐标
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为___;
(4)借助图象,写出解集
结合(1)的讨论结果,观察两个函数的图象可知:不等式x3+4x2-x-4>0的解集为___.
如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2=
| k |
| x |
观察图象可知:
①当x=-3或1时,y1=y2;
②当-3<x<0或x>1时,y1>y2,即通过观察函数的图象,可以得到不等式ax+b>
| k |
| x |
有这样一个问题:求不等式x3+4x2-x-4>0的解集.
某同学根据学习以上知识的经验,对求不等式x3+4x2-x-4>0的解集进行了探究.

下面是他的探究过程,请将(2)、(3)、(4)补充完整:
(1)将不等式按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,原不等式可以转化为x2+4x-1>
| 4 |
| x |
当x<0时,原不等式可以转化为x2+4x-1<
| 4 |
| x |
(2)构造函数,画出图象
设y3=x2+4x-1,y4=
| 4 |
| x |
双曲线y4=
| 4 |
| x |
(3)确定两个函数图象公共点的横坐标
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为___;
(4)借助图象,写出解集
结合(1)的讨论结果,观察两个函数的图象可知:不等式x3+4x2-x-4>0的解集为___.
▼优质解答
答案和解析
(2)
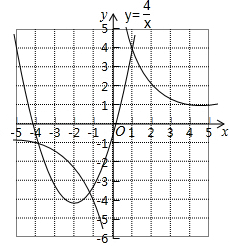 ;
;
(3)两个函数图象公共点的横坐标是±1和-4.
则满足y3=y4的所有x的值为±1和-4.
故答案是:±1和-4;
(4)不等式x3+4x2-x-4>0即当x>0时,x2+4x-1>
,此时x的范围是:x>1;
当x<0时,x2+4x-1<
,则-4<x<-1.
故答案是:x>1或-4<x<-1.
 ;
;(3)两个函数图象公共点的横坐标是±1和-4.
则满足y3=y4的所有x的值为±1和-4.
故答案是:±1和-4;
(4)不等式x3+4x2-x-4>0即当x>0时,x2+4x-1>
| 4 |
| x |
当x<0时,x2+4x-1<
| 4 |
| x |
故答案是:x>1或-4<x<-1.
看了阅读下面材料:如图1,在平面直...的网友还看了以下:
1.当要表示两双(对、副)或多双(对、副)东西时,pair要变为形式,即pairs例如:.两双鞋2 2020-06-27 …
图所示是一个电流、电压两用表的电路,电流表G的量程是100μA,内阻是1000Ω,电阻R1=0.1 2020-07-16 …
已知双曲线C:X^2/a^-Y^2/b^2=1(a>0,b>0)的一个焦点是F2(2,0),且b=根 2020-10-31 …
请问下面的问题:1.当的两个字,形成前后两个成语.忠心()()于怀2.合适的词语.()的身姿()的语 2020-11-27 …
如图1-5-15所示,一个人用双手在单杠上把自己吊起来,静止在竖直面上,在下列四种情况中,两臂用力最 2020-11-28 …
直线y=kx+1与双曲线3x^2-y^2=1相交于A,B两点,当a为何值时,A,B在双曲线的同一支上 2020-12-31 …
已知双曲线x^2/a^2-y^2/b^2=1(a>0,b>0)的左右顶点分别为A1,A2,右焦点为F 2020-12-31 …
直线y=ax+1与双曲线3x^2-y^2=1相交于A,B两点当a为何值时,A,B在双曲线的同一支上? 2020-12-31 …
直线y=ax-1与双曲线3x方-y方=1相交于A、B两点1)当a为何值时,A、B分别在双曲线的两支上 2020-12-31 …
如图所示,电源电动势电源电动势E=6内电阻r=1欧,外电路定值电阻R1=2R2=8R3=1.1.当a 2020-12-31 …