早教吧作业答案频道 -->数学-->
已知函数f(x)=2-|x|,x≤2(x-2)2,x>2,函数g(x)=b-f(2-x),其中b∈R.若函数y=f(x)-g(
题目详情
已知函数f(x)=
,函数g(x)=b-f(2-x),其中b∈R.若函数y=f(x)-g(x)恰有2个零点,则b的取值范围是___.
| |
|
▼优质解答
答案和解析
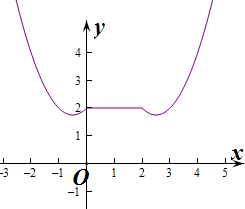 ∵g(x)=b-f(2-x),
∵g(x)=b-f(2-x),
∴y=f(x)-g(x)=f(x)-b+f(2-x),
由f(x)-b+f(2-x)=0,得f(x)+f(2-x)=b,
设h(x)=f(x)+f(2-x),
若x≤0,则-x≥0,2-x≥2,
则h(x)=f(x)+f(2-x)=2+x+x2,
若0≤x≤2,则-2≤-x≤0,0≤2-x≤2,
则h(x)=f(x)+f(2-x)=2-x+2-|2-x|=2-x+2-2+x=2,
若x>2,-x<-2,2-x<0,
则h(x)=f(x)+f(2-x)=(x-2)2+2-|2-x|=x2-5x+8.
即h(x)=
,
作出函数h(x)的图象如图:
当x≤0时,h(x)=2+x+x2=(x+
)2+
≥
,
当x>2时,h(x)=x2-5x+8=(x-
)2+
≥
,
故当b=
时,h(x)=b,有两个交点,
当b=2时,h(x)=b,有无数个交点,
由图象知要使函数y=f(x)-g(x)恰有2个零点,
即h(x)=b恰有2个根,
则满足2<b,b=
故答案为:2<b,b=
.
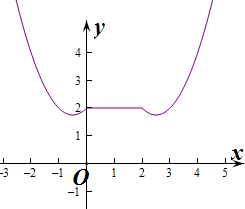 ∵g(x)=b-f(2-x),
∵g(x)=b-f(2-x),∴y=f(x)-g(x)=f(x)-b+f(2-x),
由f(x)-b+f(2-x)=0,得f(x)+f(2-x)=b,
设h(x)=f(x)+f(2-x),
若x≤0,则-x≥0,2-x≥2,
则h(x)=f(x)+f(2-x)=2+x+x2,
若0≤x≤2,则-2≤-x≤0,0≤2-x≤2,
则h(x)=f(x)+f(2-x)=2-x+2-|2-x|=2-x+2-2+x=2,
若x>2,-x<-2,2-x<0,
则h(x)=f(x)+f(2-x)=(x-2)2+2-|2-x|=x2-5x+8.
即h(x)=
|
作出函数h(x)的图象如图:
当x≤0时,h(x)=2+x+x2=(x+
| 1 |
| 2 |
| 7 |
| 4 |
| 7 |
| 4 |
当x>2时,h(x)=x2-5x+8=(x-
| 5 |
| 2 |
| 7 |
| 4 |
| 7 |
| 4 |
故当b=
| 7 |
| 4 |
当b=2时,h(x)=b,有无数个交点,
由图象知要使函数y=f(x)-g(x)恰有2个零点,
即h(x)=b恰有2个根,
则满足2<b,b=
| 7 |
| 4 |
故答案为:2<b,b=
| 7 |
| 4 |
看了已知函数f(x)=2-|x|,...的网友还看了以下:
[f(x)g(x)]'=f'(x)g(x)+f(x)g'(x)中的g(x)g‘(x)分别代表什么[ 2020-04-26 …
f(x)/g(x)>m可推出[f(x)-mg(x)]*g(x)>0.他的g(x)怎么推出来f(x) 2020-05-17 …
f(x),g(x)是D上的函数,证明inf{f(x)+g(x)}>=inf{f(x)}+inf{g 2020-06-12 …
已知f(x)、g(x)都是定义在R上的函数,g(x)≠0,f(x)g(x)=ax,且f′(x)g( 2020-06-16 …
导数乘法证明中h是什么意思?(f(x)g(x))'=lim(h→0)[f(x+h)g(x+h)-f 2020-07-22 …
关于复合函数的问题.设f(x)={0,x≤0;x,x>0这是个分段函数,下同.g(x)={0,x≤0 2020-11-01 …
考验智商极限的问题我说的问题叙述起来都不复杂:f(x),g(x)都在[0,1]上连续,而且f[g(x 2020-11-06 …
设函数f(x)=(1/3)x^3-ax(a>0),g(x)=b*x^2+2b-1第一问与23无关(2 2020-12-08 …
已知函数f(x)=x^2+1,且g(x)=f[f(x)],G(x)=g(x)-af(x)已知函数f( 2020-12-08 …
设f(x),g(x)在[a,b]上连续,在(a,b)内可导,且f'(x)=g'(x),x属于(a,b 2020-12-23 …