早教吧作业答案频道 -->数学-->
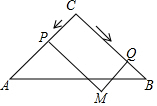
如图,在Rt△ABC中,∠C=90°、AC=BC=4,点P从点C出发沿CA以每秒1个单位长度的速度向终点A运动,同时,点Q从点C出发沿CB-BA运动,点Q在CB上的速度为每秒2个单位长度,在BA上的速度为每秒2个单
题目详情
如图,在Rt△ABC中,∠C=90°、AC=BC=4,点P从点C出发沿CA以每秒1个单位长度的速度向终点A运动,同时,点Q从点C出发沿CB-BA运动,点Q在CB上的速度为每秒2个单位长度,在BA上的速度为每秒
个单位长度,当点P到达A点时,点Q随之停止运动,以CP、CQ为邻边作▱CPMQ.设▱CPMQ与△ABC重叠部分图形的面积为y,点P的运动时间为x秒.
(1)当点M落在AB上时,求x的值.
(2)当点Q在边CB上运动时,求y与x的函数关系式
(3)直接写出在P、Q两点整个运动过程中,当▱CPMQ与△ABC重叠部分图形不是四边形时,x的取值范围.
| 2 |

(1)当点M落在AB上时,求x的值.
(2)当点Q在边CB上运动时,求y与x的函数关系式
(3)直接写出在P、Q两点整个运动过程中,当▱CPMQ与△ABC重叠部分图形不是四边形时,x的取值范围.
▼优质解答
答案和解析
(1)如图1中,
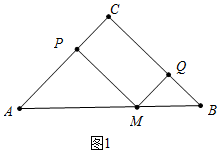
∵∠C=90°、AC=BC=4,四边形CPMQ是平行四边形,
∴四边形CPMQ是矩形,∠A=∠B=45°,
∴AB∥MQ,
∴∠MQB=∠C=90°,
∴∠QMB=∠B=45°,
∴PC=MQ=BQ,
∴2t+t=4,
∴t=
.
(2)如图2中,①当0<t≤
时,重叠部分是四边形CPMQ.
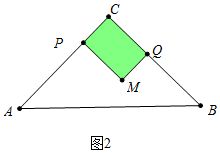
y=t•2t=2t2,
②如图3中,
<t≤2时,重叠部分是五边形CPEFQ.
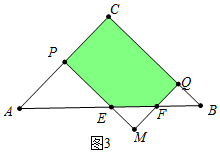
y=S四边形CPMQ-S△EFM=2t2-
(3t-4)2=-
t2+12t-8,
综上所述y=
.
(3)如图4中,当Q与B重合时,重叠部分是四边形,
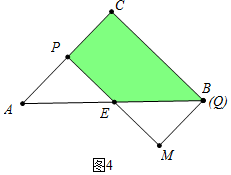
如图5中,当点P与A重合时,重叠部分是三角形.
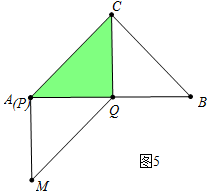
∴在P、Q两点整个运动过程中,当▱CPMQ与△ABC重叠部分图形不是四边形时,x的取值范围为
<t<2或t=4.

∵∠C=90°、AC=BC=4,四边形CPMQ是平行四边形,
∴四边形CPMQ是矩形,∠A=∠B=45°,
∴AB∥MQ,
∴∠MQB=∠C=90°,
∴∠QMB=∠B=45°,
∴PC=MQ=BQ,
∴2t+t=4,
∴t=
| 4 |
| 3 |
(2)如图2中,①当0<t≤
| 4 |
| 3 |

y=t•2t=2t2,
②如图3中,
| 4 |
| 3 |

y=S四边形CPMQ-S△EFM=2t2-
| 1 |
| 2 |
| 5 |
| 2 |
综上所述y=
|
(3)如图4中,当Q与B重合时,重叠部分是四边形,

如图5中,当点P与A重合时,重叠部分是三角形.

∴在P、Q两点整个运动过程中,当▱CPMQ与△ABC重叠部分图形不是四边形时,x的取值范围为
| 4 |
| 3 |
看了如图,在Rt△ABC中,∠C=...的网友还看了以下:
4个气缸的控制问题我想控制4个气缸,先后顺序是--气缸A推出,到位后,气缸B推出(同时气缸A缩回) 2020-05-13 …
急··要用初一的方式解不多,就3个1.关于X的方程a(a-2)X=4(a-2)求a的取值满足:(1 2020-06-27 …
(1)现有一只电子蚂蚁P到B点出发,以8个单位长度/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A 2020-06-27 …
一个3和一对4-7还有一对9和3个Q.K一个2怎么打赢一对10和一对A?不是斗地主不能出连对还有不 2020-07-04 …
逻辑与,按位与,约简与运算搞不明白例如a=4'b0101,b=4'b0011a&&B=?a||b= 2020-07-05 …
m种不同的球各n个,从中取出n个球,有多少种可能!例如:1、4个红球4个篮球,从中取出4个球,则有 2020-07-14 …
已知集合A包含于B,且A包含于C,B={0,1,2,3,4},C={0,2,4,8}则集合A的子集 2020-07-30 …
A.B.C三位同学周末结伴外出游玩.他们中午买了同样的9个面包平均分着吃,A付了5个面包的钱,B付了 2020-11-15 …
用4个4和5个0按要求组成一个九位数.(1)一个零都不读出来.(至少写2个)(2)只读出一个用4个4 2020-11-19 …
小红买售价4.4元的钢笔一支,根据你的生活经验,结合人民币币值的特点,下列付钱方式不合理的是()A. 2020-12-31 …