早教吧作业答案频道 -->数学-->
已知A，B，C三点都在体积为500π3的球O的表面上，若AB=4，∠ACB=30°，则球心O到平面ABC的距离为．
题目详情
已知A，B，C三点都在体积为
的球O的表面上，若AB=4，∠ACB=30°，则球心O到平面ABC的距离为___．
| 500π |
| 3 |
▼优质解答
答案和解析
设球的半径为R，则
=
，解得R=5．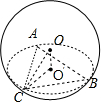
设△ABC的外接圆的半径为r，2r=
=
=8，解得r=4．
∴球心O到平面ABC的距离d=
=
=3．
故答案为：3．
| 4πR3 |
| 3 |
| 500π |
| 3 |
设△ABC的外接圆的半径为r，2r=
| AB |
| sin∠ACB |
| 4 |
| sin30° |
∴球心O到平面ABC的距离d=
| R2-r2 |
| 52-42 |
故答案为：3．
看了已知A，B，C三点都在体积为5...的网友还看了以下：
已知点A(-3,n)是反比例函数图像上的一个点,与原点O,B(3,0)围成的三角形的面积为3求反比 2020-05-16 …
设f(x)={e^x+a,x>0 3x+b,x≤0.若limx→0f(x)存在,则必有（A）b-a 2020-05-17 …
已知关于戈的方程ax2+bx+c=O（a≠0），下列说法：①若方程有两个互为相反数的实数根，则b= 2020-07-02 …
已知关于戈的方程ax2+bx+c=O（a≠0），下列说法：①若方程有两个互为相反数的实数根，则b= 2020-07-02 …
三角形ABC中三个点A(-1,O),B(5,0),C(2,5),则△ABC的形状是 2020-07-13 …
已知圆O:x2+y2=4,点P是直线X=4上的动点,若点A(-2,0),B(2,0),直线PA,P 2020-07-30 …
下列结论中，正确的是（）A.2014cm长的有向线段不可能表示单位向量B.若0是直线l上的一点，单 2020-08-02 …
请帮忙解释一下下面两道题1.设有以下一段程序chars[]="Hello";char*p=s;执行完 2020-10-30 …
（2000•宁波）如图，过⊙O外一点A向⊙O引割线AEB，ADC，DF∥BC，交AB于F．若CE过圆 2020-12-05 …
双曲线x^2／a^2－y^2／b^2＝1（a＞O,b＞0）的右支上存在一点,它到右焦点及左准线（x＝ 2020-12-31 …