早教吧作业答案频道 -->数学-->
如图,射线AM上有一点B,AB=6,点C是射线AM上异于B的一点,过C作CD⊥AM,且CD=43AC,过D点作DE⊥AD,交射线AM于E,在射线CD取点F,使得CF=CB,连接AF并延长,交DE于点G,设AC=3x.(1)当C在B点右
题目详情
如图,射线AM上有一点B,AB=6,点C是射线AM上异于B的一点,过C作CD⊥AM,且CD=
AC,过D点作DE⊥AD,交射线AM于E,在射线CD取点F,使得CF=CB,连接AF并延长,交DE于点G,设AC=3x.
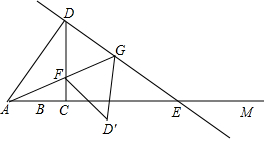
(1)当C在B点右侧时,求AD.DF的长.(用关于x的代数式表示)
(2)当x为何值时,△AFD是等腰三角形;
(3)作点D关于AG的对称点D′,连接FD′,GD′,若四边形DFD′G是平行四边形,求x的值.(直接写出答案)
| 4 |
| 3 |

(1)当C在B点右侧时,求AD.DF的长.(用关于x的代数式表示)
(2)当x为何值时,△AFD是等腰三角形;
(3)作点D关于AG的对称点D′,连接FD′,GD′,若四边形DFD′G是平行四边形,求x的值.(直接写出答案)
▼优质解答
答案和解析
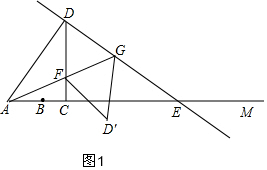 (1)∵CD=
(1)∵CD=
AC,AC=3x,
∴CD=4x,
∵CD⊥AM,
∴∠ACD=90°,
由勾股定理得:AD=5x,
∵AB=6,C在B点右侧,
∴BC=AC-AB=3x-6,
∵BC=FC=3x-6,
∴DF=CD-FC=4x-(3x-6)=x+6;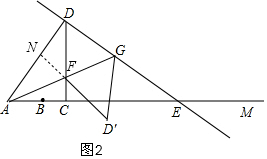
(2)分两种情况:
①当C在B点的右侧时,
∴AC>AB,
∴F必在线段CD上,
∵∠ACD=90°,
∴∠AFD是钝角,若△ADF为等腰三角形,只可能AF=DF,过F作FN⊥AD于N,如图2,
∴AN=ND=2.5x,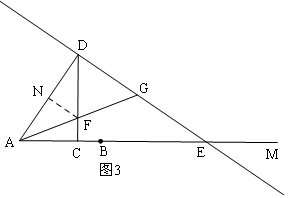
cos∠ADC=
=
,
=
,
x=
;
②当C在线段AB上时,同理可知若△ADF为等腰三角形,只可能AF=DF,
i)当CF<CD时,过F作FN⊥AD于N,如图3,
∵AB=6,AC=3x,
∴BC=CF=6-3x,
∴DF=4x-(6-3x)=7x-6,
cos∠ADC=
=
,
∴
=
,
x=
,
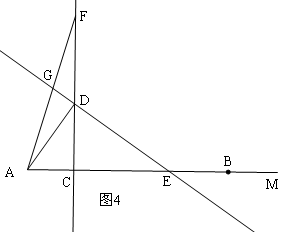
ii)当CF>CD时,如图4,
BC=CF=6-3x,
∴FD=AD=6-3x-4x=6-7x,
则6-7x=5x,
x=
,
综上所述,当x=
或
或
时,△AFD是等腰三角形;
(3)∵四边形DFD′G是平行四边形,且DF=D′F,
∴▱DFD′G是菱形,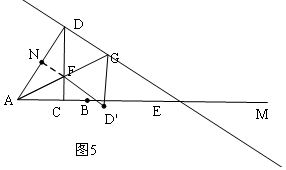
∴DF=DG,
∴∠DFG=∠DGF,
∵∠AFC=∠DFG,
∴∠DGF=∠AFC,
∵∠ACD=∠ADG=90°,
∴∠FAC=∠DAG,
即AF平分∠DAC,
过F作FN⊥AD于N,
当C在AB的延长线上时,如图2,FN=FC=3x-6,DF=x+6,
sin∠CDA=
=
,
解得:x=4,
当C在AB边上时,如图5,FN=FC=6-3x,
DF=7x-6,
sin∠CDA=
=
,
x=
,
综上所述,若四边形DFD′G是平行四边形,x的值是4或
.
 (1)∵CD=
(1)∵CD=| 4 |
| 3 |
∴CD=4x,
∵CD⊥AM,
∴∠ACD=90°,
由勾股定理得:AD=5x,
∵AB=6,C在B点右侧,
∴BC=AC-AB=3x-6,
∵BC=FC=3x-6,
∴DF=CD-FC=4x-(3x-6)=x+6;

(2)分两种情况:
①当C在B点的右侧时,
∴AC>AB,
∴F必在线段CD上,
∵∠ACD=90°,
∴∠AFD是钝角,若△ADF为等腰三角形,只可能AF=DF,过F作FN⊥AD于N,如图2,
∴AN=ND=2.5x,

cos∠ADC=
| DN |
| DF |
| DC |
| AD |
| 2.5x |
| x+6 |
| 4x |
| 5x |
x=
| 48 |
| 17 |
②当C在线段AB上时,同理可知若△ADF为等腰三角形,只可能AF=DF,
i)当CF<CD时,过F作FN⊥AD于N,如图3,
∵AB=6,AC=3x,
∴BC=CF=6-3x,
∴DF=4x-(6-3x)=7x-6,
cos∠ADC=
| DN |
| DF |
| CD |
| AD |

∴
| 2.5x |
| 7x-6 |
| 4x |
| 5x |
x=
| 48 |
| 31 |
ii)当CF>CD时,如图4,
BC=CF=6-3x,
∴FD=AD=6-3x-4x=6-7x,
则6-7x=5x,
x=
| 1 |
| 2 |
综上所述,当x=
| 48 |
| 17 |
| 48 |
| 31 |
| 1 |
| 2 |
(3)∵四边形DFD′G是平行四边形,且DF=D′F,
∴▱DFD′G是菱形,

∴DF=DG,
∴∠DFG=∠DGF,
∵∠AFC=∠DFG,
∴∠DGF=∠AFC,
∵∠ACD=∠ADG=90°,
∴∠FAC=∠DAG,
即AF平分∠DAC,
过F作FN⊥AD于N,
当C在AB的延长线上时,如图2,FN=FC=3x-6,DF=x+6,
sin∠CDA=
| 3x-6 |
| x+6 |
| 3 |
| 5 |
解得:x=4,
当C在AB边上时,如图5,FN=FC=6-3x,
DF=7x-6,
sin∠CDA=
| 6-3x |
| 7x-6 |
| 3 |
| 5 |
x=
| 4 |
| 3 |
综上所述,若四边形DFD′G是平行四边形,x的值是4或
| 4 |
| 3 |
看了如图,射线AM上有一点B,AB...的网友还看了以下:
如果在 数轴上A点和B点对应的数为a和 b,且A在原点的左边、B在原点的右边那么a-b是 什么数? 2020-04-05 …
已知aΔb=(a-b)2,a※b=(a+b)(a-b),例如,1Δ2=(1-2)2=1,1※2=( 2020-05-15 …
下列命题正确的是...在下面哦.A定义在(a,b)上的函数fx,若存在x1、x2属于(a,b),当 2020-06-04 …
设A,B为同阶方阵,且通过初等变换可以化成相同的标准形,则:A.A和B的秩相等.B.A与B合同设A 2020-06-30 …
如图,已知数轴上点A、B、C所对应的数a、b、c都不为0,且C是AB的中点.如果|a+b|-|a- 2020-07-20 …
若函数f(x)在R上可导,且f(x)>f'(x),当a>b时,下列不等式成立的是A.e^af(若函 2020-07-29 …
如图,已知数轴上点A、B、C所对应的数a、b、c都不为0,且C是AB的中点.如果|a+b|-|a-2 2020-11-01 …
分解因式谁能给我讲解下!a^n+b^n=(a+b)([a^{n-1}]-[a^{n-2}]*b+[a 2020-11-20 …
有关概率的!书上写的公式是:P(A+B)=P(A)+P(B)-P(AB)但是我想啊,A+B是指A与B 2020-11-28 …
已知a,b属于正实数a^2+b^2/2=1求y=a√(1+b^2)的最大值参考书上是用y^2=[a√ 2020-12-31 …