早教吧作业答案频道 -->数学-->
如图,在平行四边形ABCD中,AD=2AB=6cm,BE是∠ABC的角平分线,点M从点E出发,沿ED方向以1cm/s的速度向点D运动,点N从点C出发,沿射线CB方向运动,以4cm/s的运动速度,当点M运动到点D时,点N随
题目详情
如图,在平行四边形ABCD中,AD=2AB=6cm,BE是∠ABC的角平分线,点M从点E出发,沿ED方向以1cm/s的速度向点D运动,点N从点C出发,沿射线CB方向运动,以4cm/s的运动速度,当点M运动到点D时,点N随之停止运动,设运动时间为t秒.
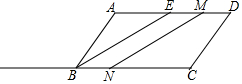
(1)求AE的长;
(2)是否存在以M、E、B、N为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.
(3)当t=___时,线段NM将平行四边形ABCD面积二等分(直接写出答案).

(1)求AE的长;
(2)是否存在以M、E、B、N为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.
(3)当t=___时,线段NM将平行四边形ABCD面积二等分(直接写出答案).
▼优质解答
答案和解析
(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEB=∠CBE,
∵BE是∠ABC的角平分线,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AE=AB,
∵2AB=6cm,
∴AE=3cm;
(2)由(1)知,AE=3,
∵AD=6,
∴DE=AD-AB=3,
由运动知,EM=t,CN=4t(0≤t≤3),
∵AD∥BC,要以M、E、B、N为顶点的四边形是平行四边形,只要EM=BN,
当点N在边BC上时,EN=BC-CN=6-4t,
∴t=6-4t,
∴t=
当点N在边CB的延长线上时,EN=CN-BC=4t-6,
∴t=4t-6,
∴t=2,
∴t=
或t=2时,以M、E、B、N为顶点的四边形是平行四边形;
(3)如图,
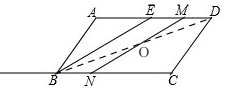
连接BD交MN于O,
∵线段NM将平行四边形ABCD面积二等分,
∴MN必过BD的中点,
∴OB=OD,
∵AD∥BC,
∴∠MDO=∠NBO,
在△MOD和△NOB中,
,
∴△MOD≌△NOB,
∴DM=BN,
由运动知,EM=t,CN=4t,
∴DM=3-t,BN=6-4t,
∴3-t=6-4t,
∴t=1,
∴t=1时,线段MN将平行四边形ABCD面积二等分,
故答案为1.
∴AD∥BC,
∴∠AEB=∠CBE,
∵BE是∠ABC的角平分线,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AE=AB,
∵2AB=6cm,
∴AE=3cm;
(2)由(1)知,AE=3,
∵AD=6,
∴DE=AD-AB=3,
由运动知,EM=t,CN=4t(0≤t≤3),
∵AD∥BC,要以M、E、B、N为顶点的四边形是平行四边形,只要EM=BN,
当点N在边BC上时,EN=BC-CN=6-4t,
∴t=6-4t,
∴t=
| 6 |
| 5 |
当点N在边CB的延长线上时,EN=CN-BC=4t-6,
∴t=4t-6,
∴t=2,
∴t=
| 6 |
| 5 |
(3)如图,

连接BD交MN于O,
∵线段NM将平行四边形ABCD面积二等分,
∴MN必过BD的中点,
∴OB=OD,
∵AD∥BC,
∴∠MDO=∠NBO,
在△MOD和△NOB中,
|
∴△MOD≌△NOB,
∴DM=BN,
由运动知,EM=t,CN=4t,
∴DM=3-t,BN=6-4t,
∴3-t=6-4t,
∴t=1,
∴t=1时,线段MN将平行四边形ABCD面积二等分,
故答案为1.
看了 如图,在平行四边形ABCD中...的网友还看了以下:
已知抛物线C:y=x2-4x+3.(1)求该抛物线关于y轴对称的抛物线C1的解析式.(2)将抛物线 2020-07-09 …
三个导体元件A、B、C的伏安特性曲线分别如图线a、b、c所示.当它们串联后接在6V稳压直流电源两端 2020-07-15 …
在空间直角坐标系中,x=1的所有点构成的图形是A.点B.直线C.平面D.线段 2020-07-20 …
4、下列说法正确的是()A水平放置的正方形的直观图可能是梯形B两条相交直线的直观图可能是平行直线C 2020-08-01 …
如图已知直线a在平面α内,直线b在平面α内,a∥b,直线c∥平面α,a与c是异面直线,求证b,c是 2020-08-02 …
下面四个命题,正确的是()A.己知直线a,b⊂平面α,直线c⊂平面β,若c⊥a,c⊥b,则平面α⊥平 2020-11-02 …
如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=40°,若使直线b与直线c平行 2020-11-03 …
(2014•长春)如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若使 2020-11-03 …
2009向量小题,告急!2009年广东卷文)已知平面向量a=(x,1),b=(-x,x^2),则向量 2020-12-19 …
直线a与直线c平行,直线b也与直线c平行,那么直线a与b互相平行.(判断对错) 2021-01-11 …