早教吧作业答案频道 -->数学-->
如图1,在边长为2的正方形ABCD中,P是对角线BD上的动点,点E在射线AD上,且PA=PE.(1)求证:PC=PE;(2)求∠EPC的度数;(3)如图2,把正方形ABCD改为边长为2的菱形ABCD,且∠ABC=120°,其他
题目详情
如图1,在边长为2的正方形ABCD中,P是对角线BD上的动点,点E在射线AD上,且PA=PE.
(1)求证:PC=PE;
(2)求∠EPC的度数;
(3)如图2,把正方形ABCD改为边长为2的菱形ABCD,且∠ABC=120°,其他条件不变,连接CE,求AP•CE的最小值.
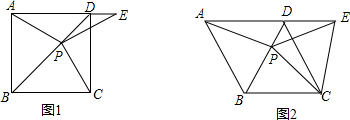
(1)求证:PC=PE;
(2)求∠EPC的度数;
(3)如图2,把正方形ABCD改为边长为2的菱形ABCD,且∠ABC=120°,其他条件不变,连接CE,求AP•CE的最小值.

▼优质解答
答案和解析
(1)证明:在正方形ABCD中,AB=BC,
∠ABP=∠CBP=45°,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PE,
∴∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°-∠PFC-∠PCF=180°-∠DFE-∠E,
即∠CPF=∠EDF=90°;
(3)在菱形ABCD中,AB=BC,∠ABP=∠CBP=60°,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP,
∵PA=PE,
∴PC=PE,
∴∠DAP=∠DCP,
∵PA=PC,
∴∠DAP=∠AEP,
∴∠DCP=∠AEP
∵∠CFP=∠EFD(对顶角相等),
∴180°-∠PFC-∠PCF=180°-∠DFE-∠AEP,
即∠CPF=∠EDF=180°-∠ADC=180°-120°=60°,
∴△EPC是等边三角形,
∴PC=CE,
∴AP=CE,
当AP•CE的值最小时,则AP最小,由垂线段最短可知当AP⊥BD时,AP最小,此时AP=
=
,
∴AP•CE的最小值=
×
=3.
∠ABP=∠CBP=45°,
在△ABP和△CBP中,
|
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PE,
∴∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°-∠PFC-∠PCF=180°-∠DFE-∠E,
即∠CPF=∠EDF=90°;
(3)在菱形ABCD中,AB=BC,∠ABP=∠CBP=60°,
在△ABP和△CBP中,
|
∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP,
∵PA=PE,
∴PC=PE,
∴∠DAP=∠DCP,
∵PA=PC,
∴∠DAP=∠AEP,
∴∠DCP=∠AEP
∵∠CFP=∠EFD(对顶角相等),
∴180°-∠PFC-∠PCF=180°-∠DFE-∠AEP,
即∠CPF=∠EDF=180°-∠ADC=180°-120°=60°,
∴△EPC是等边三角形,
∴PC=CE,
∴AP=CE,
当AP•CE的值最小时,则AP最小,由垂线段最短可知当AP⊥BD时,AP最小,此时AP=
| AB2-BP2 |
| 3 |
∴AP•CE的最小值=
| 3 |
| 3 |
看了 如图1,在边长为2的正方形A...的网友还看了以下:
如图,在矩形ABCD中,AB=7,BC=3,E在AD上,且AE=2,在边AB上是否存在点P,使得P 2020-05-16 …
如图,四边形ABCD是平行四边形,点E、F分别为AD、BC边上的点,且AE=CF求证:四边形BED 2020-05-16 …
设a>0,f(x)=(e^x/a)+(a/e^x)在R上的图像关于y轴对称;求:①求a的值.②求证 2020-06-03 …
扇形拱高是什么弧长是什么半径是A,弧形在正方形里,正方形边长A,弧形面积怎么求?原题:已知正方形边 2020-07-10 …
高数的几道小题一、求函数f(x)=(1+x)^[x/tan(x-兀)]在区间(0,2兀)内的间断点 2020-07-13 …
已知a>0,函数f(x)=e^x/a+a/e^x在R上满足f(-x)=f(x),其中e为自然对数的 2020-08-02 …
f(x)=x/[a+e^(bx)]在(-∞,+∞)内连续,为什么必须a≤0,b>0a≤0和b>0是如 2020-11-01 …
lim[1+(-1)^n/n]的1/sin[sqrt(1+n^2*PI)]n->无穷这个题目怎么算呢 2020-11-01 …
a.e.ay在哪些单词里发I不要字母组合请示例 2020-11-23 …
已知:如图,点E、F分别是平行四边形ABCD的边AD、BC的中点,且AD=2AB,分别联结AF、DF 2020-12-07 …