早教吧作业答案频道 -->数学-->
如图,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.(1)当PC=CE时,求∠CDP的度数;(2)试用等式表示线段PB、BC、CE之间的数量关系,并证明.
题目详情
如图,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.
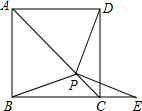
(1)当PC=CE时,求∠CDP的度数;
(2)试用等式表示线段PB、BC、CE之间的数量关系,并证明.

(1)当PC=CE时,求∠CDP的度数;
(2)试用等式表示线段PB、BC、CE之间的数量关系,并证明.
▼优质解答
答案和解析
(1)∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠BCP=∠DCP=45°,∠BCD=∠DCE=90°,
∴∠PCE=45°+90°=135°,
在△BCP和△DCP中,
,
∴△BCP≌△DCP(SAS),
∴BP=DP,∠CBP=∠CDP,
∵PE=PB,PC=CE,
∴PD=PE,∠CBP=∠PEB=∠CPE=
(180°-135°)=22.5°,
∴∠CDP=22.5°;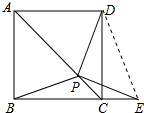
(2)BC2+CE2=2PB2,理由如下:
连接DE,如图所示:
由(1)得:∠CBP=∠CDP,PD=PE,
∵PB=PE,
∴∠CBP=∠PEB,
∴∠CDP=∠PEB,
∴P、C、E、D四点共圆,
∴∠DPE=∠DCE=90°,
由勾股定理得:DE2=CD2+CE2,DE2=PD2+PE2,
∵BC=CD,PB=PD=PE,
∴BC2+CE2=2PB2.
∴AB=BC=CD=AD,∠BCP=∠DCP=45°,∠BCD=∠DCE=90°,
∴∠PCE=45°+90°=135°,
在△BCP和△DCP中,
|
∴△BCP≌△DCP(SAS),
∴BP=DP,∠CBP=∠CDP,
∵PE=PB,PC=CE,
∴PD=PE,∠CBP=∠PEB=∠CPE=
| 1 |
| 2 |
∴∠CDP=22.5°;

(2)BC2+CE2=2PB2,理由如下:
连接DE,如图所示:
由(1)得:∠CBP=∠CDP,PD=PE,
∵PB=PE,
∴∠CBP=∠PEB,
∴∠CDP=∠PEB,
∴P、C、E、D四点共圆,
∴∠DPE=∠DCE=90°,
由勾股定理得:DE2=CD2+CE2,DE2=PD2+PE2,
∵BC=CD,PB=PD=PE,
∴BC2+CE2=2PB2.
看了 如图,在正方形ABCD中,P...的网友还看了以下:
阅读下面的文字,完成需题。用思想“照亮”人生——心地光明的当代君子叶朗孙焘74岁的叶朗先生还在给学 2020-05-16 …
这个是证明的:当x∈(0,√(b/a))时,x1x2 2020-05-23 …
关于饼干的发明的英语作文,150词左右,感激不尽.如上所述参考资料:饼干最早是英国人发明的,当时叫 2020-06-08 …
(2014•安徽)设实数c>0,整数p>1,n∈N*.(Ⅰ)证明:当x>-1且x≠0时,(1+x) 2020-06-11 …
设U(x)=(x1,x2)={a1x1^P+a2x2^p}^1/p,这个是常见的常替代弹性效用函数 2020-07-13 …
已知椭圆x^2/a^2+y^2/b^2=1的离心率为根号3/3,过右焦点F的直线l与C相交于AB两 2020-08-01 …
已知A是数域P上的n*n矩阵,设W1={AX|X∈P^n},W2={X|X∈P^n,AX=0}证明: 2020-10-31 …
2008年奥运会于北京时间8月8日20时正式开幕。在美国纽约(西五区)留学的小明收看了开幕式的直播, 2020-12-05 …
在古代,我们的祖先发明的当时最先进的计算工具是什么? 2020-12-08 …
(二)实用类文本阅读(14分)阅读下面的文字,完成7—9题。用思想“照亮”人生——心地光明的当代君子 2020-12-19 …