早教吧作业答案频道 -->数学-->
在平面直角坐标系xOy中,抛物线y=mx2-2mx+n(m<0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴正半轴交于点D,连接AD并延长交x轴于E,连AC、DC.S△DEC:S△AEC=3:4.(1)求点E的
题目详情
在平面直角坐标系xOy中,抛物线y=mx2-2mx+n(m<0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴正半轴交于点D,连接AD并延长交x轴于E,连AC、DC.S△DEC:S△AEC=3:4.
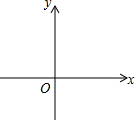
(1)求点E的坐标;
(2)△AEC能否为直角三角形?若能,求出此时抛物线的函数表达式;若不能,请说明理由.

(1)求点E的坐标;
(2)△AEC能否为直角三角形?若能,求出此时抛物线的函数表达式;若不能,请说明理由.
▼优质解答
答案和解析
(1)如图所示:设此抛物线对称轴与x轴交于点F,
∴S△DEC:S△AEC=DO:AF=3:4,
∵DO∥AF,
∴△EDO∽△EAF,
∴EO:EF=DO:AF=3:4,
∴EO:OF=3:1,
由y=mx2-2mx+n(m<0)得:A(1,n-m),D(0,n),
∴OF=1,
∴EO=3,
∴E(-3,0);
(2)∵DO:AF=3:4,
∴
=
,
∴n=-3m,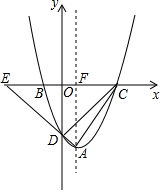
∴y=mx2-2mx-3m=m(x2-2x-3)
=m(x-3)(x+1),
∴B(-1,0),C(3,0),A(1,-4m),
由题意可知,AE,AC不可能与x轴垂直,
∴若△AEC为直角三角形,则∠EAC=90°,
又∵AF⊥EC,可得△EFA∽△AFC,
∴
=
,即
=
,
∵m<0,
∴m=-
,
∴二次函数解析式为:y=-
x2+
x+
.
∴S△DEC:S△AEC=DO:AF=3:4,
∵DO∥AF,
∴△EDO∽△EAF,
∴EO:EF=DO:AF=3:4,
∴EO:OF=3:1,
由y=mx2-2mx+n(m<0)得:A(1,n-m),D(0,n),
∴OF=1,
∴EO=3,
∴E(-3,0);
(2)∵DO:AF=3:4,
∴
| n |
| n-m |
| 3 |
| 4 |
∴n=-3m,

∴y=mx2-2mx-3m=m(x2-2x-3)
=m(x-3)(x+1),
∴B(-1,0),C(3,0),A(1,-4m),
由题意可知,AE,AC不可能与x轴垂直,
∴若△AEC为直角三角形,则∠EAC=90°,
又∵AF⊥EC,可得△EFA∽△AFC,
∴
| EF |
| AF |
| AF |
| CF |
| 4 |
| -4m |
| -4m |
| 2 |
∵m<0,
∴m=-
| ||
| 2 |
∴二次函数解析式为:y=-
| ||
| 2 |
| 2 |
3
| ||
| 2 |
看了 在平面直角坐标系xOy中,抛...的网友还看了以下:
初二下册分式难题小明与小亮在一条东西向的马路边上,从同一地点出发向东跑步,速度分别为v1=1.5m 2020-05-13 …
求均减速度计算方法已知A点速度为V1,B点速度为V2,A点到B点的距离为S,求A到B的减速度. 2020-05-22 …
一质量为m的滑雪者从A点由静止沿粗糙曲面滑下,到B点后水平飞离B点.空间几何尺寸如图所示,滑雪者从 2020-05-23 …
SELECT (52)A.A,R.C,F,GB.A,C,S.B,S.FC.A,C,S.B,S.CD. 2020-05-26 …
一质量为m的滑雪者从A点由静止沿粗糙曲面滑下,到B点后水平飞离B点.空间几何尺寸如图所示,滑雪者从 2020-06-04 …
一个质点沿直线做加速运动,到A点时速度为3m/s,到B点时速度变为12m/s历时6s;到B点后又做 2020-06-27 …
如图,线段AB=20cm.(1)点P沿线段AB自A点向B点以2厘米/秒运动,同时点Q沿线段BA自B 2020-07-22 …
1.从A点和B点测得上海东方明珠塔顶电视塔C的仰角分别为38.3°和50°,AB=200m,求电视塔 2020-11-13 …
1.从A点和B点测得上海东方明珠电视塔顶C的仰角分别是38.3°和50°,AB=200mi.求东方明 2020-11-13 …
一平面简谐波以400m/s的波速在均匀介质中沿一直线从A点向B点传播.已知直线上质点A的振动周期为0 2020-12-09 …