早教吧作业答案频道 -->数学-->
在等边三角形ABC的边BC上任取一点D,以CD为边向外作等边三角形CDE(如图①),连接AD,BE,易证明BE=AD.(1)若点D在射线BC上(如图②),其他条件均不变,BE=AD是否依然成立?试说明理由
题目详情
在等边三角形ABC的边BC上任取一点D,以CD为边向外作等边三角形CDE(如图①),连接AD,BE,易证明BE=AD.
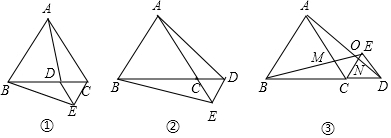
(1)若点D在射线BC上(如图②),其他条件均不变,BE=AD是否依然成立?试说明理由;
(2)在图②中,若等边三角形CDE与等边三角形ABC均在直线BC的同一侧(如图③),并且B,C,D三点在同一直线上,猜想BE=AD是否依然成立?试说明理由;
(3)在(2)的条件下,根据图汇总所标字母,请直接写出你发现的两个正确结论.
①___;②___.

(1)若点D在射线BC上(如图②),其他条件均不变,BE=AD是否依然成立?试说明理由;
(2)在图②中,若等边三角形CDE与等边三角形ABC均在直线BC的同一侧(如图③),并且B,C,D三点在同一直线上,猜想BE=AD是否依然成立?试说明理由;
(3)在(2)的条件下,根据图汇总所标字母,请直接写出你发现的两个正确结论.
①___;②___.
▼优质解答
答案和解析
(1)BE=AD依然成立,
证明:∵△ABC是等边三角形,
∴CA=CB,
∵△CDE是等边三角形,
∴CD=CE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE,
∴BE=AD;
(2)BE=AD成立,
∵△ABC是等边三角形,△CDE是等边三角形,
∴CA=CB,CD=CE,∠ACB=∠ECD=60°,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
,
∴△BCE≌△ACD,
∴BE=AD;
(3)∵△BCE≌△ACD,
∴∠DAC=∠EBC,
∠AOB=∠EBC+∠ADC=∠EBC+∠BEC=60°,
故答案为:①∠DAC=∠EBC;②∠AOB=60°.
证明:∵△ABC是等边三角形,
∴CA=CB,
∵△CDE是等边三角形,
∴CD=CE,
在△ACD和△BCE中,
|
∴△ACD≌△BCE,
∴BE=AD;
(2)BE=AD成立,
∵△ABC是等边三角形,△CDE是等边三角形,
∴CA=CB,CD=CE,∠ACB=∠ECD=60°,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
|
∴△BCE≌△ACD,
∴BE=AD;
(3)∵△BCE≌△ACD,
∴∠DAC=∠EBC,
∠AOB=∠EBC+∠ADC=∠EBC+∠BEC=60°,
故答案为:①∠DAC=∠EBC;②∠AOB=60°.
看了 在等边三角形ABC的边BC上...的网友还看了以下:
一道关于初一全等的几何题,应该不算太难如图,三角形ABC中,角BAC=90,D为三角形内一点,且A 2020-05-13 …
如图在三角形abc中ba等于bc角c等于120,ab的垂直平分线de交ac于点d.求角a的度数若a 2020-05-16 …
以下试题最好用初中知识解答,实在不行再用四点共圆.图略.如图在等边三角形ABC的边BC上任取一点D 2020-06-06 …
如图△A′B′C′是△ABC的直观图,其中A′B′=A′C,那么△ABC是()A.等腰三角形B.直 2020-06-27 …
如图,直观图所示的平面图形是[]A.正三角形B.锐角三角形C.钝角三角形D.直角三角形 2020-06-27 …
已知A={三角形}B={等腰三角形}C={等边三角形}D={直角三角形}用维恩图表示他们之间的关系 2020-07-12 …
如图,点D是△ABC的边BC上一点,如果AB=AD=2,AC=4,且BD:DC=2:3,则△ABC 2020-07-26 …
如图在三角形abc中ab等于ac,AD垂直BC,垂足为D,三角形ABC的周长是36CM如图在三角形 2020-07-30 …
1:如图直线AB,CD相交于点O,EO垂直于AB,O点为垂点,OF平角AOC且角EOC=2/5角A 2020-07-30 …
(2011•广元)小明通过实验研究光从水中射入空气中的现象,如图是他根据实验现象画的光路图.改变入射 2020-11-12 …