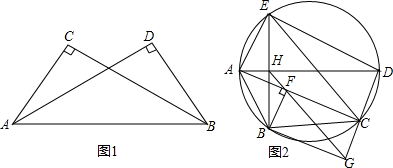
（本题证明值可直接利用如下结论：若公共边所对的两个张角相等，则相应的四点共圆．例如如图1，由∠ACB=∠ADB，可得四点A、B、C、D共圆）如图2，圆内接五边形ABCDE中，AD是外接圆的

Question

（本题证明值可直接利用如下结论：若公共边所对的两个张角相等，则相应的四点共圆．例如如图1，由∠ACB=∠ADB，可得四点A、B、C、D共圆）如图2，圆内接五边形ABCDE中，AD是外接圆的直径，BE⊥AD，垂足为H，过点H作平行于CE的直线，与直线AC，DC分别交于F，G．证明：
（1）点A，B，F，H共圆；
（2）四边形BFCG是矩形．

Answer 1

考点：
四点共圆
专题：

分析：
（1）根据圆周角定理得出，∠BAF=∠BEC，结合平行线的性质得出∠BAF=∠BHF，即可得出答案；（2）根据四点共圆的性质得出∠BFG=∠DAB=∠BCG，进而得出B、G、F、H共圆，即可得出BG⊥GC，进而得出答案．

证明：（1）由HG∥CE，得∠BHF=∠BEC，又∵BC=BC，∴∠BAF=∠BEC，∴∠BAF=∠BHF，∴点A、B、F、H共圆；（2）由（1）的结论，得∠BHA=∠BFA，∵BE⊥AD，∴BF⊥AC，又∵AD是圆的直径，∴CG⊥AC，由A、B、C、D共圆及A、B、F、H共圆，∴∠BFG=∠DAB=∠BCG，∴B、G、F、H共圆，∴∠BGC=∠AFB=90°，∴BG⊥GC，∴四边形BFCG是矩形．
点评：
此题主要考查了四点共圆的性质以及四点共圆的证明，正确应用四点共圆的性质是解题关键．