O的半径为r，它的内接正三角形、正方形、正六边形的边长分别为a，b，c．（1）求a，b，c；（2）以a，b，c为边可否构成三角形？如果能，构成的是什么三角形？如果不能，请说明理由．

Question

O的半径为r，它的内接正三角形、正方形、正六边形的边长分别为a，b，c．
（1）求a，b，c；
（2）以a，b，c为边可否构成三角形？如果能，构成的是什么三角形？如果不能，请说明理由．

Answer 1

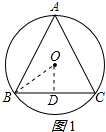（1）如图1所示，
在正三角形ABC中，连接OB，过O作OD⊥BC于D，
则∠OBC=30°，BD=OB•cos30°=(√(3))/(2)r，
故a=BC=2BD=√(3)r；
如图2所示，
在正方形ABCD中，连接OB、OC，过O作OE⊥BC于E，
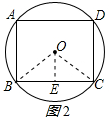则△OBE是等腰直角三角形，
2BE²=OB²，即BE=(√(2))/(2)r，
故b=BC=√(2)r；
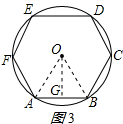
如图3所示，
在正六边形ABCDEF中，连接OA、OB，过O作OG⊥AB，
则△OAB是等边三角形，
故AG=OA•cos60°=(1)/(2)r，
c=AB=2AG=r；
（2）能构成三角形，构成直角三角形；理由如下：
∵a=√(3)r，b=√(2)r，c=r，
∴c²+b²=a²，
∴能构成直角三角形．