早教吧作业答案频道 -->数学-->
如图,BD是⊙O的直径,四边形ABCD是⊙O的内接四边形,且AB=AC,AH⊥BD于点H,延长CD至点E.(1)求证:∠ADE=∠ADB;(2)求证:BH=HD+CD;(3)若DC=3DH,试求tan∠ADE和sin∠BDC的值.
题目详情
如图,BD是⊙O的直径,四边形ABCD是⊙O的内接四边形,且AB=AC,AH⊥BD于点H,延长CD至点E.
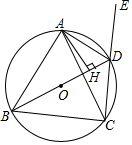
(1)求证:∠ADE=∠ADB;
(2)求证:BH=HD+CD;
(3)若DC=3DH,试求tan∠ADE和sin∠BDC的值.

(1)求证:∠ADE=∠ADB;
(2)求证:BH=HD+CD;
(3)若DC=3DH,试求tan∠ADE和sin∠BDC的值.
▼优质解答
答案和解析
(1)∵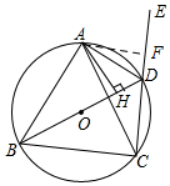 四边形ABCD是⊙O的内接四边形,
四边形ABCD是⊙O的内接四边形,
∴∠ADF=∠ABC,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠ACB=∠ADB,
∴∠ADE=∠ADB;
(2)过点A作AF⊥CE于点F,
∵∠ADE=∠ADB,AH⊥BD,
∴AH=AF,DH=DF,
在Rt△ABH与Rt△ACF中,
∴Rt△ABH≌Rt△ACF(HL)
∴BH=CF,
∵CF=CD+DF=CD+DH,
∴BH=HD+CD,
(3)设DH=1,
∴DC=3,
∴BH=DC+DH=4,
∵BD是⊙O的直径,
∴∠BAD=∠BCD=90°
∵∠ABH+∠BAH=∠BAH+∠DAH=90°,
∴∠ABH=∠DAH,
∴△ABH∽△DAH
∴AH2=BH•DH=4,
∴AH=2,
∴tan∠ADE=tan∠ADH=
=2,
∵BD=BH+DH=5,
∴由勾股定理可知:BC=4,
∴sin∠BDC=
=
 四边形ABCD是⊙O的内接四边形,
四边形ABCD是⊙O的内接四边形,∴∠ADF=∠ABC,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠ACB=∠ADB,
∴∠ADE=∠ADB;
(2)过点A作AF⊥CE于点F,
∵∠ADE=∠ADB,AH⊥BD,
∴AH=AF,DH=DF,
在Rt△ABH与Rt△ACF中,
|
∴Rt△ABH≌Rt△ACF(HL)
∴BH=CF,
∵CF=CD+DF=CD+DH,
∴BH=HD+CD,
(3)设DH=1,
∴DC=3,
∴BH=DC+DH=4,
∵BD是⊙O的直径,
∴∠BAD=∠BCD=90°
∵∠ABH+∠BAH=∠BAH+∠DAH=90°,
∴∠ABH=∠DAH,
∴△ABH∽△DAH
∴AH2=BH•DH=4,
∴AH=2,
∴tan∠ADE=tan∠ADH=
| AH |
| DH |
∵BD=BH+DH=5,
∴由勾股定理可知:BC=4,
∴sin∠BDC=
| BC |
| BD |
| 4 |
| 5 |
看了 如图,BD是⊙O的直径,四边...的网友还看了以下:
如图所示的直角坐标系中,四边形ABCD各个顶点的坐标分别为A(-1,3),B(-3,2),C(-4 2020-04-27 …
描述下列诗句所体现的意境(1)四面边声连角起,千嶂里,长烟落日孤城闭(2)风住尘香花已尽,日晚倦梳 2020-05-13 …
1.设a.b.c分别是三角形ABC的三条边,且a/b=a+1/a+b+c,是判断∠A,∠B的关系. 2020-05-13 …
1、解方程组:2x-3y=-1{(1/2)x-(1/3)y=-(3/2)2、平行四边形的周长为40 2020-07-03 …
1.四边形ABCD和四边形A'B'C'D'中,AB:A'B'=BC:B'C'=CB:C'D'=DA 2020-07-25 …
如图四边形的两条对角线互相垂直,我们把这种四边形叫做勾股四边形勾股四边形ABCD的两条边长a=6, 2020-08-03 …
一个四边形的周长是48CM,已知第一条边长是A,第二条边比第一条边的2倍长3CM,第三条边长等于第一 2020-11-24 …
四边形的判定一个四边形的周长是48cm,已知第一条边长是acm,第二条边比第一条边的2倍长3cm,第 2020-11-24 …
ABCD四名学生按任意次序站成一排,试求下列事件的概率1、A在边上2、A和B都在边上ABCD四名学生 2020-12-05 …
如果四边形ABCD和四边形A'B'C'D'是位似图形,且位似比是K,下列成立的是()1,AC/A'C 2020-12-25 …