早教吧作业答案频道 -->数学-->
已知△ABC和△ADE都是等边三角形,点B,D,E同一在一条直线上.(1)如图1,当AC⊥DE,且AD=2时,求线段BC的长度;(2)如图2,当且CD⊥BE时,取线段BC的中点F,线段DC的中点G,连接DF,EG,
题目详情
已知△ABC和△ADE都是等边三角形,点B,D,E同一在一条直线上.
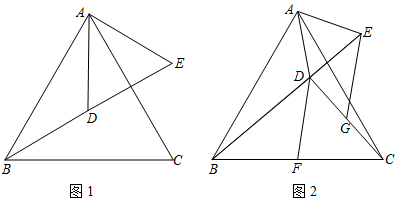
(1)如图1,当AC⊥DE,且 AD=2时,求线段BC的长度;
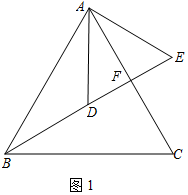
(2)如图2,当且CD⊥BE时,取线段BC的中点F,线段DC的中点G,连接DF,EG,求证:DF=EG.

(1)如图1,当AC⊥DE,且 AD=2时,求线段BC的长度;
(2)如图2,当且CD⊥BE时,取线段BC的中点F,线段DC的中点G,连接DF,EG,求证:DF=EG.
▼优质解答
答案和解析
 (1) 如图1所示:
(1) 如图1所示:
∵△ABC和△ADE都是等边三角形,AC⊥DE,AD=2,
∴BC=AC,DE=AD=2,DF=
DE=1,AF=CF,
∴AF=
=
,
∴AC=2AF=2
,
∴BC=2
;
(2)证明:连接CE,如图2所示:
∵ABC和△ADE都是等边三角形,点B,D,E同一在一条直线上.
∴AB=AC,AD=AE,∠BAC=∠DAE=∠AED=60°,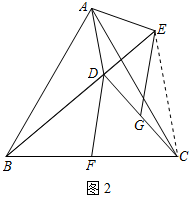
∴∠ADB=120°,∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠AEC=∠ADB=120°,
∴∠CED=∠AEC-∠AED=60°,
∵CD⊥BE,
∴∠DCE=30°,
∴DE=
CE,
∵线段BC的中点为F,线段DC的中点为G,
∴FG∥BD,FG=
BD,
∴FG∥DE,FG=DE,
∴四边形DFGE是平行四边形,
∴DF=EG.
 (1) 如图1所示:
(1) 如图1所示:∵△ABC和△ADE都是等边三角形,AC⊥DE,AD=2,
∴BC=AC,DE=AD=2,DF=
| 1 |
| 2 |
∴AF=
| AD2-DF2 |
| 3 |
∴AC=2AF=2
| 3 |
∴BC=2
| 3 |
(2)证明:连接CE,如图2所示:
∵ABC和△ADE都是等边三角形,点B,D,E同一在一条直线上.
∴AB=AC,AD=AE,∠BAC=∠DAE=∠AED=60°,

∴∠ADB=120°,∠BAD=∠CAE,
在△ABD和△ACE中,
|
∴△ABD≌△ACE(SAS),
∴BD=CE,∠AEC=∠ADB=120°,
∴∠CED=∠AEC-∠AED=60°,
∵CD⊥BE,
∴∠DCE=30°,
∴DE=
| 1 |
| 2 |
∵线段BC的中点为F,线段DC的中点为G,
∴FG∥BD,FG=
| 1 |
| 2 |
∴FG∥DE,FG=DE,
∴四边形DFGE是平行四边形,
∴DF=EG.
看了 已知△ABC和△ADE都是等...的网友还看了以下:
几ˋˊ何数学题自己先把图画出来吧图:一个由点A.B.C组成的等边三角形中,点D是边AB的中点,点E 2020-05-13 …
有一张四边形纸片ABCD,∠B=∠D=90°,把制片按照如图所示方法折叠,使点B落在AD边上的G点 2020-05-16 …
如图,平行四边形ABCD中,AE=CG,DH=BF,连结E,F,G,H,E,则四边形EFHG是?如 2020-05-16 …
任意画一个四边形ABCD,四边形的四边中心分别为E,F,G,H,连接EF,FG,GH,HE,并量出 2020-05-16 …
将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E交BC于F,边AB折叠后与BC边 2020-05-17 …
过四边形ABCD的对角线交点O画CD的平行线,分别与边BC,AD及AB的延长线交与E,F,G,求证 2020-05-17 …
设G=为无环的无向图,|V|=6,|E|=16,则G是()A.完全图B.零图C.D.多重图设A和B 2020-06-12 …
一道关于离散数学中图论部分的问题证明:若边e在G的某一闭迹中,则e在G的某一圈中 2020-06-19 …
如图,边长为6cm的正方形ABCD中,点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时 2020-06-21 …
如何判断一条边是否位于多面体内部、外部?在三维空间中,给定一条边e的端点坐标,以及一个由多个三角面 2020-06-27 …