早教吧作业答案频道 -->数学-->
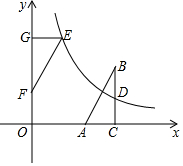
如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数y=kx(k>0)的图象经过BC边的中点D(3,1)(1)求这个反比例函数的表达式;(2)若△ABC与△EFG成中心对称
题目详情
如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数y=
(k>0)的图象经过BC边的中点D(3,1)
(1)求这个反比例函数的表达式;
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
①求OF的长;
②连接AF,BE,证明四边形ABEF是正方形.
| k |
| x |

(1)求这个反比例函数的表达式;
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
①求OF的长;
②连接AF,BE,证明四边形ABEF是正方形.
▼优质解答
答案和解析
(1)∵反比例函数y=
(k>0)的图象经过点D(3,1),
∴k=3×1=3,
∴反比例函数表达式为y=
;
(2)①∵D为BC的中点,
∴BC=2,
∵△ABC与△EFG成中心对称,
∴△ABC≌△EFG,
∴GF=BC=2,GE=AC=1,
∵点E在反比例函数的图象上,
∴E(1,3),即OG=3,
∴OF=OG-GF=1;
②如图,连接AF、BE,
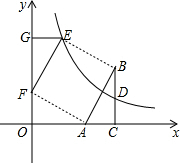
∵AC=1,OC=3,
∴OA=GF=2,
在△AOF和△FGE中
∴△AOF≌△FGE(SAS),
∴∠GFE=∠FAO=∠ABC,
∴∠GFE+∠AFO=∠FAO+∠BAC=90°,
∴EF∥AB,且EF=AB,
∴四边形ABEF为平行四边形,
∴AF=EF,
∴四边形ABEF为菱形,
∵AF⊥EF,
∴四边形ABEF为正方形.
(1)∵反比例函数y=
| k |
| x |
∴k=3×1=3,
∴反比例函数表达式为y=
| 3 |
| x |
(2)①∵D为BC的中点,
∴BC=2,
∵△ABC与△EFG成中心对称,
∴△ABC≌△EFG,
∴GF=BC=2,GE=AC=1,
∵点E在反比例函数的图象上,
∴E(1,3),即OG=3,
∴OF=OG-GF=1;
②如图,连接AF、BE,

∵AC=1,OC=3,
∴OA=GF=2,
在△AOF和△FGE中
|
∴△AOF≌△FGE(SAS),
∴∠GFE=∠FAO=∠ABC,
∴∠GFE+∠AFO=∠FAO+∠BAC=90°,
∴EF∥AB,且EF=AB,
∴四边形ABEF为平行四边形,
∴AF=EF,
∴四边形ABEF为菱形,
∵AF⊥EF,
∴四边形ABEF为正方形.
看了 如图,在直角坐标系中,Rt△...的网友还看了以下:
mysql查询求助:一个非常困难的问题有2个表:表A:字段typeqtymark(值为yes或no 2020-04-26 …
a1=(1,2,0)T,a2=(1,a+2,-3a)T,a3=(-1,-b-2,a+2b)T,β= 2020-07-09 …
如图,在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,且a、b满足|a+2|+( 2020-07-10 …
EXCEL中,表A为汇总表,表B为明细表.求表B中与表A名称相同的行,数量、金额求和公式.EXCE 2020-07-23 …
如图,在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,且a、b满足|a+2|+( 2020-08-03 …
在三角形中,已知a=7,b=5.C=45度,求c,A,B.(用反三角函数表示)在三角形中,已知a= 2020-08-03 …
设已知全集S集合A={x2x+5>1},B={x2-x>1}化简集合A与B并用区间表示求A交B和A并 2020-11-01 …
(1)已知数轴上的点A表示数+3,数轴上的点B表示数-3,试求A,B之间的距离;(2)已知数轴上点A 2020-11-08 …
[紧急求助]1.在我国代表人民行使当家作主的权利的是:A人大代表B各级人民代表大会2.冷战结束的标志 2020-12-03 …
已知数轴上有三点A,B,C,其中A表示的数为-5,B表示7,C点在A,B之间,且AB=BC(甲的速度 2020-12-23 …