如图，设A是棱长为2的正方体的一个顶点，过从顶点A出发的三条棱的中点作截面，对正方体的所有顶点都如此操作，截去8个三棱锥，所得的各截面与正方体各面共同围成一个多面体，则关于

Question

如图，设A是棱长为2的正方体的一个顶点，过从顶点A出发的三条棱的中点作截面，对正方体的所有顶点都如此操作，截去8个三棱锥，所得的各截面与正方体各面共同围成一个多面体，则关于此多面体有以下结论：
①有24个顶点；②有36条棱；③有14个面；④表面积为12；⑤体积为

(20)/(3)．
正确的有（　　）个．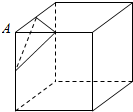

A. 1

B. 2

C. 3

D. 4

Answer 1

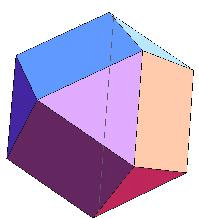如图，原来的六个面还在只不过是变成了一个小正方形，
再添了八个顶点各对应的一个三角形的面，
所以总计6+8=14个面，故③正确；
每个正方形4条边，每个三角形3条边，4×6+3×8=48，
考虑到每条边对应两个面，所以实际只有(1)/(2)×48=24条棱．故②错误；
所有的顶点都出现在原来正方体的棱的中点位置，
原来的棱的数目是12，所以现在的顶点的数目是12．
或者从图片上可以看出每个顶点对应4条棱，每条棱很明显对应两个顶点，
所以顶点数是棱数的一半即12个．故①错误；
三角形和四边形的边长都是(√(2))/(2)a，
所以正方形总面积为6×(1)/(2)a²=3a²，三角形总面积为8×(1)/(2)×(1)/(2)a²sin60°=√(3)a²，
表面积（3+√(3)）a²，故④错；
体积为原正方形体积减去8个三棱锥体积，每个三棱锥体积为8×(1)/(6)（(a)/(2)）³=(1)/(6)a³，剩余总体积为a³-(1)/(6)a³=(5)/(6)a³．⑤正确．
故选：B．