早教吧作业答案频道 -->数学-->
如图,直线y=-2x与直线y=kx+b相交于点A(a,2),并且直线y=kx+b经过x轴上点B(2,0)(1)求直线y=kx+b的解析式.(2)求两条直线与y轴围成的三角形面积.(3)直接写出不等式(k+2)x+b≥0
题目详情
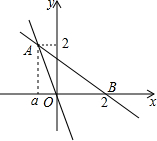
如图,直线y=-2x 与直线y=kx+b 相交于点A(a,2),并且直线y=kx+b经过x轴上点B(2,0)
(1)求直线y=kx+b的解析式.
(2)求两条直线与y轴围成的三角形面积.
(3)直接写出不等式(k+2)x+b≥0的解集.

(1)求直线y=kx+b的解析式.
(2)求两条直线与y轴围成的三角形面积.
(3)直接写出不等式(k+2)x+b≥0的解集.
▼优质解答
答案和解析
(1)把A(a,2)代入y=-2x中,得-2a=2,
∴a=-1,
∴A(-1,2)
把A(-1,2),B(2,0)代入y=kx+b中得
,
∴k=-
,b=
,
∴一次函数的解析式是y=-
x+
;
(2)设直线AB与Y轴交于点C,则C(0,
)
∴S△BOC=
×
×1=
;
(3)不等式(k+2)x+b≥0可以变形为kx+b≥-2x,
结合图象得到解集为:x≥-1.
∴a=-1,
∴A(-1,2)
把A(-1,2),B(2,0)代入y=kx+b中得
|
∴k=-
| 2 |
| 3 |
| 4 |
| 3 |
∴一次函数的解析式是y=-
| 2 |
| 3 |
| 4 |
| 3 |
(2)设直线AB与Y轴交于点C,则C(0,
| 4 |
| 3 |
∴S△BOC=
| 1 |
| 2 |
| 4 |
| 3 |
| 2 |
| 3 |
(3)不等式(k+2)x+b≥0可以变形为kx+b≥-2x,
结合图象得到解集为:x≥-1.
看了 如图,直线y=-2x与直线y...的网友还看了以下:
已知函数f(x)=sin(ωx+φ),(ω>0),f(x)图象相邻最高点和最低点的横坐标相差π2, 2020-05-13 …
设随机变量X的概率分布密度为f(x)=12e-|x|,-∞<x<+∞.(1)求X的数学期望EX和方 2020-06-10 …
(2012•宣城模拟)在平面直角坐标系下,已知C1:x=mty=1−t(t为参数,m≠0的常数), 2020-07-26 …
直线x+3y=0绕原点按顺时针方向旋转30°,所得直线与圆(x-2)2+y2=3的位置关系是()A 2020-07-26 …
圆(x-2)2+y2=3与直线x-y-2=0的位置关系是()A.相交且过圆心B.相交但不过圆心C. 2020-07-31 …
关于x的方程x-2m=-3x+4与2-x=m的解互为相反数.(1)求m的值;(2)求这两个方程的解 2020-07-31 …
下列各组函数,表示相等函数的是()A.f(x)=x,g(x)=x2B.f(x)=x2−4x−2,g 2020-08-02 …
设两个变量x和y之间具有线性相关关系,它们的相关系数为r,y关于x的回归直线方程为̂y=kx+b,则 2020-08-02 …
赋值语句“x=x+1”的正确解释为()A.x的值与x+1的值可能相等B.将原来x的值加上1后,得到的 2020-11-01 …
(2008•乐山二模)已知R元素的相对原子质量m与其原子核内的质子数和中子数之和在数值上相等.若R2 2020-11-12 …