早教吧作业答案频道 -->数学-->
如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.(1)求证:BC∥平面DEF;(2)求多面体D-BCEF的体积.
题目详情
如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.
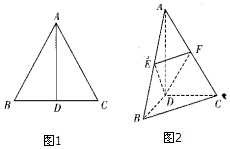
(1)求证:BC∥平面DEF;
(2)求多面体D-BCEF的体积.

(1)求证:BC∥平面DEF;
(2)求多面体D-BCEF的体积.
▼优质解答
答案和解析
证明:(1)因为点E,F分别是AB,AC的中点,所以EF∥BC.
又因为BC⊄平面DEF,EF⊂平面DEF,
所以BC∥平面DEF. …(5分)
(2)依题意,AD⊥BD,AD⊥CD,且BD∩DC=D,
所以AD⊥平面BCD,
又因为二面角B-AD-C为直二面角,所以BD⊥CD,
所以V三棱锥A-BCD=
S△BCD•AD=
×
×1×1×
=
,
V三棱锥F-ADE=
S△ADE•
CD=
×
×
×
×
×1=
,
所以VD-BCFE=V三棱锥A-BCD-V三棱锥F-ADE=
-
=
. …(12分)
又因为BC⊄平面DEF,EF⊂平面DEF,
所以BC∥平面DEF. …(5分)
(2)依题意,AD⊥BD,AD⊥CD,且BD∩DC=D,
所以AD⊥平面BCD,
又因为二面角B-AD-C为直二面角,所以BD⊥CD,
所以V三棱锥A-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 6 |
V三棱锥F-ADE=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 24 |
所以VD-BCFE=V三棱锥A-BCD-V三棱锥F-ADE=
| ||
| 6 |
| ||
| 24 |
| ||
| 8 |
看了 如图,边长为2的等边三角形A...的网友还看了以下:
有一个长方体形状的物品,长、宽、高分别为a,b,c(a>b>c>0),有三种不同的捆扎方法,如图所有 2020-03-30 …
如图,已知△ABC和点P.(1)画△ABC关于点P的对称图形△A′B′C′;(2)过点P任意画一条 2020-05-02 …
如图所示的图象是直线ax+by+c=0的图象,则下列条件中正确的为()A.a=b,c=0B.a=- 2020-06-03 …
如图A’B’平行BA,B’C’平行CB,C'A'平行AC,〈ABC与〈B'有什么关系?线段AB'与 2020-08-02 …
已知正数abc,且a/b+c=b/c+a=c/a+b=k.则在下列四个点中,在正比例函数y=kx图像 2020-11-01 …
左图为某区域甲地的一个居住小区图片,右图为该区域等温线示意图,回答各小题。1.据图判断a、b、c、d 2020-11-02 …
如何用尺规画图法画两个全等三角形?)(1)已知△ABC,AB=3,BC=4,CA=5.用尺规作图法做 2020-12-02 …
已知二次函数y=ax平方+bx+c,(1)若a=2,b+c=-2,b>c,且二次函数的图像经过点(p 2020-12-08 …
下表是某同学对细胞周期不同表示方法的总结,你认为错误的选项是()选项方法名称表示方法结论A扇形图A→ 2020-12-10 …
如图所示的电机模型中,属于交流发电机和直流发电机的分别是如()A.图(b)和图(a)B.图(c)和图 2020-12-13 …