已知异面直线a，b所成角为60°，直线AB与a，b均垂直，且垂足分别是点A，B若动点P∈a，Q∈b，|PA|+|QB|=m，则线段PQ中点M的轨迹围成的区域的面积是．

Question

已知异面直线a，b所成角为60°，直线AB与a，b均垂直，且垂足分别是点A，B若动点P∈a，Q∈b，|PA|+|QB|=m，则线段PQ中点M的轨迹围成的区域的面积是___．

Answer 1

设线段AB的中垂面为α，则M的轨迹在平面α内，在平面α内分别作直线a，b的投影a′，b′，则两直线的夹角为60°．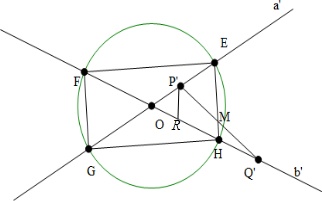
设A，B在平面α的投影为O，P，Q在平面α内的投影分别为P′，Q′，则M为P′Q′的中点，
∴OP′=PA，OQ′=BQ．
∵|PA|+|QB|=m，∴OP′+OQ′=m．
在直线a′，b′上分别取点E，F，G，H四点，使得OE=OF=OG=OH=(m)/(2)．
∵OE+OH=OP′+OQ′=m，∴P′E=HQ′，
过P′作P′R∥EH交OQ′于R，则HR=P′E=HQ′，
∴P′Q′的中点M在EH上，
同理可得M在EF，FG，GH上，
∴M的轨迹为矩形EHGH．
∵∠EOH=60°，OE=OF=OG=OH=(m)/(2)，
∴S_矩形EFGH=(1)/(2)×(m)/(2)×(m)/(2)×sin60°×2+(1)/(2)×(m)/(2)×(m)/(2)×sin120°×2=(√(3)m2)/(4)．
故答案为：(√(3)m2)/(4)．