早教吧作业答案频道 -->数学-->
如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.(1)求证:AC是O的切线;(2)若OB=10,CD=8,求BE的长.
题目详情
如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
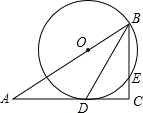
(1)求证:AC是 O的切线;
(2)若OB=10,CD=8,求BE的长.

(1)求证:AC是 O的切线;
(2)若OB=10,CD=8,求BE的长.
▼优质解答
答案和解析
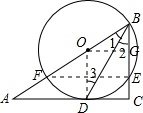 (1)证明:连接OD,
(1)证明:连接OD,
∵BD为∠ABC平分线,
∴∠1=∠2,
∵OB=OD,
∴∠1=∠3,
∴∠2=∠3,
∴OD∥BC,
∵∠C=90°,
∴∠ODA=90°,
则AC为圆O的切线;
(2) 过O作OG⊥BC,
∴四边形ODCG为矩形,
∴GC=OD=OB=10,OG=CD=8,
在Rt△OBG中,利用勾股定理得:BG=6,
∴BC=BG+GC=6+10=16,
∵OD∥BC,
∴△AOD∽△ABC,
∴
=
,即
=
,
解得:OA=
,
∴AB=
+10=
,
连接EF,
∵BF为圆的直径,
∴∠BEF=90°,
∴∠BEF=∠C=90°,
∴EF∥AC,
∴
=
,即
=
,
解得:BE=12.
 (1)证明:连接OD,
(1)证明:连接OD,∵BD为∠ABC平分线,
∴∠1=∠2,
∵OB=OD,
∴∠1=∠3,
∴∠2=∠3,
∴OD∥BC,
∵∠C=90°,
∴∠ODA=90°,
则AC为圆O的切线;
(2) 过O作OG⊥BC,
∴四边形ODCG为矩形,
∴GC=OD=OB=10,OG=CD=8,
在Rt△OBG中,利用勾股定理得:BG=6,
∴BC=BG+GC=6+10=16,
∵OD∥BC,
∴△AOD∽△ABC,
∴
| OA |
| AB |
| OD |
| BC |
| OA |
| OA+10 |
| 10 |
| 16 |
解得:OA=
| 50 |
| 3 |
∴AB=
| 50 |
| 3 |
| 80 |
| 3 |
连接EF,
∵BF为圆的直径,
∴∠BEF=90°,
∴∠BEF=∠C=90°,
∴EF∥AC,
∴
| BE |
| BC |
| BF |
| AB |
| BE |
| 16 |
| 20 | ||
|
解得:BE=12.
看了 如图,在Rt△ABC中,∠C...的网友还看了以下:
图①是以AB为直径的半圆形纸片,AB=6cm,…………图①是以AB为直径的半圆形纸片,AB=6cm 2020-05-15 …
如图,BD是直径,过圆O上一点A作圆O切线交DB延长线于P,过点B作BC平行PA交圆O于C,连接A 2020-06-06 …
如图,已知角A、O、B=90°,角B、O、C=30°,OM平分角AOC,ON平分角B、O、C.1. 2020-06-18 …
如图所示在等腰三角行ABC中,AB=AC,角BAC=50度,角BAC的平分线与AB的中垂线交于点O 2020-07-09 …
如图,⊙O的半径为1,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥CD,点M是直线CD上异于 2020-07-20 …
(2014•塘沽区二模)如图,⊙O的半径为1,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥C 2020-07-20 …
写一个正则表达式DN验证类CN=ASOUOLSTDCSNEC=CN规则要求1.必须CN=开头2.必 2020-07-23 …
公式里面缺少;是什么意思这个公式是在股票里用的:如下:MA13:=MA(C,13);MA34:=M 2020-07-23 …
如图,AB是圆圈O的直径,AB=10,DC切⊙O于C,DC切⊙O于点C,AD⊥DC,垂足为D,AD 2020-07-30 …
如图:⊙O和⊙O'内切于P半径OA和OB切⊙O'于C、D连O'C和O'D如果两圆半径分别为9和3则 2020-07-31 …