早教吧作业答案频道 -->数学-->
完成下列推理说明:(1)如图1,已知∠1=∠2,∠B=∠C,可推出AB∥CD.理由如下:因为∠1=∠2(已知),且∠1=∠4()所以∠2=∠4(等量代换)所以CE∥BF()所以∠=∠3()又因为
题目详情
完成下列推理说明:
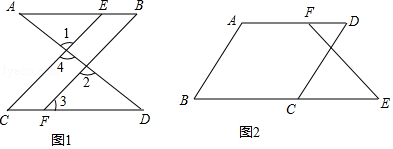
(1)如图1,已知∠1=∠2,∠B=∠C,可推出AB∥CD.理由如下:
因为∠1=∠2(已知),且∠1=∠4(___)
所以∠2=∠4(等量代换)
所以CE∥BF(___)
所以∠___=∠3(___)
又因为∠B=∠C(已知)
所以∠3=∠B(等量代换)
所以AB∥CD(___)
(2)如图2,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.
证明:∵∠B+∠BCD=180°( 已知 ),
∴AB∥CD (___)
∴∠B=___(___)
又∵∠B=∠D( 已知 ),
∴∠___=∠___ (等量代换)
∴AD∥BE(___)
∴∠E=∠DFE(___)
(1)如图1,已知∠1=∠2,∠B=∠C,可推出AB∥CD.理由如下:
因为∠1=∠2(已知),且∠1=∠4(___)
所以∠2=∠4(等量代换)
所以CE∥BF(___)
所以∠___=∠3(___)
又因为∠B=∠C(已知)
所以∠3=∠B(等量代换)
所以AB∥CD(___)
(2)如图2,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.
证明:∵∠B+∠BCD=180°( 已知 ),
∴AB∥CD (___)
∴∠B=___(___)
又∵∠B=∠D( 已知 ),
∴∠___=∠___ (等量代换)
∴AD∥BE(___)
∴∠E=∠DFE(___)

▼优质解答
答案和解析
 (1)理由:
(1)理由:
因为∠1=∠2(已知),且∠1=∠4(对顶角相等),
所以∠2=∠4(等量代换),
所以CE∥BF(同位角相等,两直线平行),
所以∠C=∠3(两直线平行,同位角相等),
又因为∠B=∠C(已知),
所以∠3=∠B(等量代换),
所以AB∥CD(内错角相等,两直线平行);
故答案为:对顶角相等,同位角相等,两直线平行,C,两直线平行,同位角相等,内错角相等,两直线平行;
(2)证明:∵∠B+∠BCD=180°(已知),
∴AB∥CD (同旁内角互补,两直线平行),
∴∠B=∠DCE(两直线平行,同位角相等),
又∵∠B=∠D(已知),
∴∠DCE=∠D (等量代换),
∴AD∥BE(内错角相等,两直线平行),
∴∠E=∠DFE(两直线平行,内错角相等).
故答案为:同旁内角互补,两直线平行,∠DCE,两直线平行,同位角相等,DCE,D,内错角相等,两直线平行,两直线平行,内错角相等.
 (1)理由:
(1)理由:因为∠1=∠2(已知),且∠1=∠4(对顶角相等),
所以∠2=∠4(等量代换),
所以CE∥BF(同位角相等,两直线平行),
所以∠C=∠3(两直线平行,同位角相等),
又因为∠B=∠C(已知),
所以∠3=∠B(等量代换),
所以AB∥CD(内错角相等,两直线平行);
故答案为:对顶角相等,同位角相等,两直线平行,C,两直线平行,同位角相等,内错角相等,两直线平行;
(2)证明:∵∠B+∠BCD=180°(已知),
∴AB∥CD (同旁内角互补,两直线平行),
∴∠B=∠DCE(两直线平行,同位角相等),
又∵∠B=∠D(已知),
∴∠DCE=∠D (等量代换),
∴AD∥BE(内错角相等,两直线平行),
∴∠E=∠DFE(两直线平行,内错角相等).
故答案为:同旁内角互补,两直线平行,∠DCE,两直线平行,同位角相等,DCE,D,内错角相等,两直线平行,两直线平行,内错角相等.
看了 完成下列推理说明:(1)如图...的网友还看了以下:
某二倍体植物的体细胞中染色体数为24,基因型为AaBb,这两对基因遵循自由组合定律,请根据图完成问 2020-06-10 …
某种羊的性别决定为XY型.已知其有角和无角由位于常染色体上的等位基因(N/n)控制;黑毛和白毛由等 2020-06-23 …
括号的成语使用错误的原因1.为了提高工作效率,必须杜绝正事不干,见人就(侃侃而谈)的工作作风2.张 2020-06-27 …
下列那些市政府设立郊野公园和海岸公园的原因?1.为市民提供休息和玩耍的地方2.保护陆上和海洋生物3 2020-06-30 …
回答问题:(1)图1表示对雌果蝇眼形的遗传研究结果,由图分析,果蝇眼形由正常眼转变为棒状眼是因为X染 2020-11-02 …
先天性行为是由因素决定的,学习行为是由因素为基础,因素的作用,由和获得. 2020-11-25 …
人类有多种血型系统,MN血型和Rh血型是其中的两种.MN血型由常染色体上的1对等位基因M、N控制,M 2020-12-24 …
人类有多种血型系统,MN血型和Rh血型是其中的两种。MN血型由常染色体上的1对等位基因M、N控制,M 2020-12-24 …
(1)图1表示对果蝇眼形的遗传研究结果,由图分析,果蝇眼形由正常眼转变为棒状眼是因为,该变化属于.雄 2020-12-25 …
图为某单基因遗传病的家系图,由第Ⅰ代至第Ⅲ代的生育过程中没有发生基因突变.如果Ⅲ1患有该遗传病的概率 2020-12-25 …