拓广探索探索“互相垂直的两直线y1=k1x+b（k1≠0）与y2=k2x+m（k2≠0）的比例系数之间的关系”（1）如图1，在平面直角坐标系xOy中，正方形OABC的边长为4，且OA，OC分别在x轴、y轴上，则对角线OB

Question

拓广探索
探索“互相垂直的两直线y₁=k₁x+b（k₁≠0）与y₂=k₂x+m（k₂≠0）的比例系数之间的关系”
（1）如图1，在平面直角坐标系xOy中，正方形OABC的边长为4，且OA，OC分别在x轴、y轴上，则对角线OB所在直线的解析式为___，对角线AC所在直线的解析式为___．

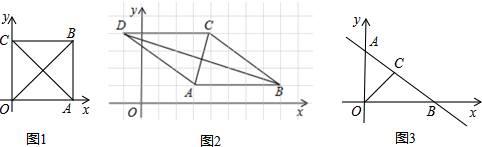
（2）边长为5的菱形ABCD如图2放置在网格中（网格的小正方形边长为1），且顶点都在格点上，分别求对角线BD所在直线、对角线AC所在直线的解析式；
（3）结合（1）（2）的解答，或者改变一下菱形ABCD的位置继续探究
①请猜想：如果两直线y₁=k₁x+b（k₁≠0）与y₂=k₂x+m（k₂≠0）互相垂直，那么k₁•k₂=___；
②请直接利用①的猜想结果解决下列问题：在平面直角坐标系中，如图3，直线y=- (1)/(2)x+5与x轴交于点B，与y轴交于点A，OC是AB边上的高，C为垂足，则点C的坐标是___．

Answer 1

（1）∵正方形OABC的边长为4，且OA，OC分别在x轴、y轴上，
∴OA=OC=AB=BC=4，
∴A（4，0），B（4，4），C（0，4）．
∴直线OB解析式为y=x，
直线AC解析式为y=-x+4，
故答案为y=x，y=-x+4，
（2）由网格知，A（3，1），B（8，1），C（4，4），D（-1，4），
设直线AC解析式为y=kx+b，
∴

3k+b=1

4k+b=4

，
∴

k=3

b=-8

，
∴直线AC的解析式为y=3x-8，
同理：直线BD解析式为y=-(1)/(3)x+(11)/(3)，
（3）①由（1）知，直线AC解析式为y=-x+4，直线OB解析式为y=x，且AC⊥BD，得出，k₁•k₂=-1
由（2）知，直线AC解析式为y=3x-8，直线BD解析式为y=-(1)/(3)x+(11)/(3)，且AC⊥BD，得出k₁•k₂=-1，
∴如果两直线y₁=k₁x+b（k₁≠0）与y₂=k₂x+m（k₂≠0）互相垂直，那么k₁•k₂=-1，
故答案为-1，
②∵OC是AB边上的高，且直线AB解析式为y=-(1)/(2)x+5①，
∴直线OC解析式为y=2x②，
联立①②得，

x=2

y=4

，
∴C（2，4），
故答案为（2，4）．