已知正四棱柱ABCD—A1B1C1D1的底面边长为2，侧棱长为，(1)求二面角B1-AC-B的大小；(2)求点B到平面AB1C的距离.

Question

已知正四棱柱ABCD—A ₁ B ₁ C ₁ D ₁ 的底面边长为2，侧棱长为 ，

(1)求二面角B ₁ -AC-B的大小；

(2)求点B到平面AB ₁ C 的距离.

Answer 1

解析:(1)连结AC、BD交于点O，连结B ₁ O(如图)，易知BB ₁ ⊥底面ABCD且BO⊥AC，

∴B ₁ O⊥AC.

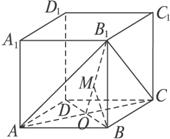
∴∠B ₁ OB是二面角B ₁ ACB的平面角.

在Rt△B ₁ BO中，B ₁ B= ，OB= ×2= .

∴tan∠B ₁ OB=1，且∠B ₁ OB为锐角.

∴∠B ₁ OB=45°，

即二面角B ₁ ACB为45°.

(2)作BM⊥B ₁ O于M，由AC⊥平面B ₁ OB，

∴BM⊥AC.∴BM⊥平面AB ₁ C ，即BM为点B到平面AB ₁ C 的距离.

在等腰Rt△B ₁ BO中，BB ₁ = ，OB= ，∴BM=1.

小结：在正棱柱中 侧棱垂直于底面 底面是正多边形 这是正棱柱的性质.本题由于底面ABCD是正方形 ∴BO⊥AC.又B ₁ B⊥底面ABCD，∴∠B ₁ OB是二面角B ₁ ACB的平面角.求点B到平面AB ₁ C 的距离 就是求Rt△B ₁ OB的斜边B ₁ O上的高.