如图10，在直角坐标系中，直线与双曲线（x＞0）相交于P（1，m）.（1）求k的值；（2）若点Q与点P关于y=x成轴对称，则点Q的坐标为Q（）；（3）若过P、Q两点的抛物线与y轴
如图10，在直角坐标系中，直线
与双曲线
（x＞0）相交于P（1，m）.
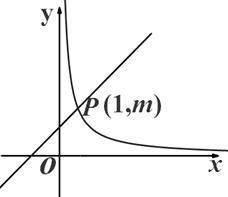（1）求k的值；
（2）若点Q与点P关于y=x成轴对称，则点
Q的坐标为Q（ ）；
（3）若过P、Q两点的抛物线与y轴的交点为
N（0，
），求该抛物线的解析式，并求出抛物
线的对称轴方程.
图10
考点：一次函数、反比例函数与二次函数。
解析：（1）把P（1，m）代入
，得
，
∴P（1，2）
把（1，2）代入
，得
，
（2）（2，1）
（3）设抛物线的解析式为
，得：
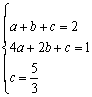，解得
，
，
∴
，
∴对称轴方程为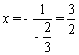
.
x^2-y^2=a^2右准线交实轴于P,过P直线交双曲线A、B,过右焦点F引直线垂直AB交双曲线于 2020-04-08 …
点P是直线y=0.5x+2与双曲线y=k/x在第一象限内的一个交点,直线y=0.5x+2与x轴y轴 2020-05-12 …
直线y=1/2+1分别交x轴.y轴与点A.C,点P事直线AC与双曲线y=k/x在第一象限内的交点, 2020-05-21 …
点P是直线y=1/2x+2与双曲线y=k/x在第一象限内的一个交点,直线y=1/2x+2与x轴、y 2020-05-21 …
如图,已知双曲线y1=1/x（x>0）,y2=k/x（x>0）,点p为双曲线y2=k/x上的一动点 2020-06-15 …
一道数学几何中考题在等腰梯形ABCD中,AD平行于BC,AB=CD,AD=3,BC=9,tan角A 2020-07-20 …
在平面直角坐标系中,A(0,2),B(0,3),过点B作直线l平行x轴,p(a,3)是直线l上的动 2020-07-30 …
一道关于双曲线的数学题中心在原点,焦点在x轴上的双曲线的实轴长是6,虚轴长是8,（1）求双曲线的方 2020-07-30 …
如图所示,点P是直线y=x+2与双曲线y=x分之k在第一象限内的一个交点如图,点P是直线y=+2与 2020-08-01 …
已知点P双曲线x2-y28=1右支上一点，F1、F2分别为双曲线的左、右焦点，I为△PF1F2的内心 2020-12-31 …