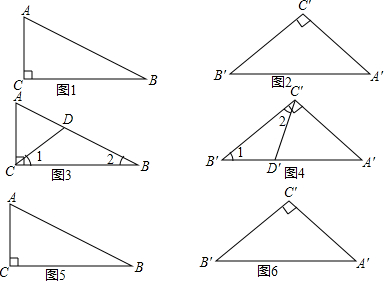
如图1和图2，在△ABC和△A′B′C′，其中∠C=∠C′=90°，且两个三角形不相似．问：能否分别用一条直线分割这两个三角形，使△ABC所分割成的两个三角形与△A′B′C′所分割成的两个三角形

Question

如图1和图2，在△ABC和△A′B′C′，其中∠C=∠C′=90°，且两个三角形不相似．问：能否分别用一条直线分割这两个三角形，使△ABC所分割成的两个三角形与△A′B′C′所分割成的两个三角形分别对应相似？如果能，请设计出分割方案；如果不能，请说明理由．
问题解决
小华通过分割∠C和∠C′，解决了问题，示意图3和图4如下（图中∠DCB=∠B′；∠D′C′B′=∠B：）
小阳说：不分割∠C和∠C′，也能解决问题．请你尝试根据小阳的解决思路解决问题．（在所给图形（图5和图6）上画出分割线，并注明相等的角即可）
结论推广
小冯发现：对于有一个角相等的两个不相似的三角形，一定可以把每一个三角形分割成两个小三角形，使分割的两个小三角形分别对应相似．请对他的发现作出解释．
深入研究
小鹏还发现：对于三角都不相等的两个三角形，不可以把每一个三角形分割成两个小三角形，使分割出的小三角形分别对应相似．
请你继续探索，对于三角都不相等的两个三角形，可以把三角形分割成三个小三角形，使分割出的小三角形分别对应相似吗？如果可以，请设计出分割方案（画出示意图或说明操作步骤）；如果不可以，请说明理由．

Answer 1

问题解决
如图a，∠C=∠C′=90°，不妨设∠CAB>∠A′，∠C′B′A′>∠B．

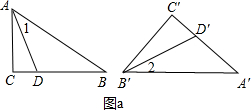
作∠DAB=∠A′（即∠1=∠A′），作∠D′B′A′=∠B（即∠2=∠B），
则有△ADB∽△A′D′B′．
∵∠ADC=∠1+∠B=∠A′+∠2=∠B′D′C′，∠C=∠C′，
∴△ACD∽△B′C′D′；

结论推广
如图b，∠C=∠C′≠90°，不妨设∠CAB>∠A′，∠C′B′A′>∠B．

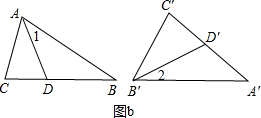
作∠DAB=∠A′（即∠1=∠A′），作∠D′B′A′=∠B（即∠2=∠B），
即可得到△ADB∽△A′D′B′．
∵∠ADC=∠1+∠B=∠A′+∠2=∠B′D′C′，∠C=∠C′，
∴△ACD∽△B′C′D′；

深入研究
如图c，不妨设∠CAB>∠A′，∠C′B′A′>∠B．

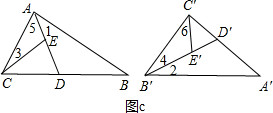
作∠DAB=∠A′（即∠1=∠A′），作∠D′B′A′=∠B（即∠2=∠B），
即可得到△ADB∽△A′D′B′．
不妨设∠ACD>∠C′B′D′，∠B′C′D′>∠CAD，
作∠ACE=∠C′B′D′（即∠3=∠4），作∠E′C′B′=∠EAC（即∠6=∠5），
即可得到△ACE∽△C′B′E′．
又因为∠EDC=∠1+∠B=∠A′+∠2=∠E′D′C′，∠CED=∠3+∠5=∠4+∠6=∠C′E′D′，
即可得到△CED∽△C′E′D′．