如图，若△ABC的周长为1，它的3条中位线组成一个新的三角形，记作△A1B1C1，△A1B1C1的3条中位线又组成一个新的三角形，记作△A2B2C2（如图所示），…，以此类推，求△A2017B2017C2017的周长是

Question

如图，若△ABC的周长为1，它的3条中位线组成一个新的三角形，记作△A₁B₁C₁，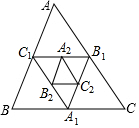
△A₁B₁C₁的3条中位线又组成一个新的三角形，记作△A₂B₂C₂ （如图所示），…，以此类推，求△A₂₀₁₇B₂₀₁₇C₂₀₁₇的周长是___．

Answer 1

∵B₁C₁、A₁C₁、A₁B₁是△A₁B₁C₁的3条中位线，
∴B₁C₁、=(1)/(2)BC，A₁C₁=(1)/(2)AC，A₁B₁=(1)/(2)AB，
∴△A₁B₁C₁的周长=(1)/(2)，
同理△A₂B₂C₂，的周长=（(1)/(2)）²，
以此类推，△A₂₀₁₇B₂₀₁₇C₂₀₁₇的周长为（(1)/(2)）²⁰¹⁷，
故答案为：（(1)/(2)）²⁰¹⁷．