早教吧作业答案频道 -->数学-->
如图,已知抛物线y=-x2+2x+3与坐标轴交于A,B,C三点,抛物线上的点D与点C关于它的对称轴对称.(1)直接写出点D的坐标和直线AD的解析式;(2)点E是抛物线上位于直线AD上方的动点,过点E
题目详情
如图,已知抛物线y=-x2+2x+3与坐标轴交于A,B,C三点,抛物线上的点D与点C关于它的对称轴对称.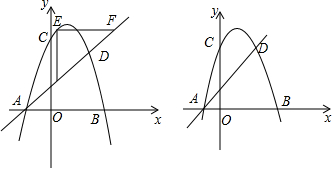
(1)直接写出点D的坐标和直线AD的解析式;
(2)点E是抛物线上位于直线AD上方的动点,过点E分别作EF∥x轴,EG∥y轴并交直线AD于点F、G,求△EFG周长的最大值;
(3)若点P为y轴上的动点,则在抛物线上是否存在点Q,使得以A,D,P,Q为顶点的四边形是平行四边形?若存在,请求出点Q的坐标,若不存在,请说明理由.
(1)直接写出点D的坐标和直线AD的解析式;
(2)点E是抛物线上位于直线AD上方的动点,过点E分别作EF∥x轴,EG∥y轴并交直线AD于点F、G,求△EFG周长的最大值;
(3)若点P为y轴上的动点,则在抛物线上是否存在点Q,使得以A,D,P,Q为顶点的四边形是平行四边形?若存在,请求出点Q的坐标,若不存在,请说明理由.
▼优质解答
答案和解析
(1)将x=0代入得y=3,
∴C(0,3).
∵抛物线的对称轴为x=-
=1,C(0,3),
∴D(2,3).
把y=0代入抛物线的解析式得:0=-x2+2x+3,解得x=3或x=-1,
∴A(-1,0).
设直线AD的解析式为y=kx+b,将点A和点D的坐标代入得:
,解得:k=1,b=1,
∴直线AD的解析式为y=x+1.
(2)如图1所示:
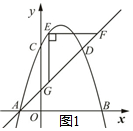
∵直线AD的解析式为y=x+1,
∴∠DAB=45°.
∵EF∥x轴,EG∥y轴,
∴∠GEF=90°,∠GFE=∠DAB=45°
∴△EFG是等腰直角三角形.
∴△EFG的周长=EF+FG+EG=(2+
)EG.
依题意,设E(t,-t2+2t+3),则G(t,t+1).
∴EG=-t2+2t+3-(t+1)=-(t-
)2+
.
∴EG的最大值为
.
∴△EFG的周长的最大值为
+
.
(3)存在.
①以AD为平行四边形的边时,PQ∥AD,PQ=AD.
∵A,D两点间的水平距离为3,
∴P,Q两点间的水平距离也为3.
∴点Q的横坐标为3或-3.
将x=3和x=-3分别代入y=-x2+2x+3得y=0或y=-12.
∴Q(3,0)或(-3,-12).
②当AD为平行四边形的对角线时,设AD的中点为M,
∵A(-1,0),D(2,3),M为AD的中点,
∴M(
,
).
设点Q的横坐标为x,则
=
,解得x=1,
∴点Q的横坐标为1.
将x=1代入y=-x2+2x+3得y=4.
∴这时点Q的坐标为(1,4).
综上所述,当点Q的坐标为Q(3,0)或(-3,-12)或(1,4)时,以A,D,P,Q为顶点的四边形是平行四边形.
∴C(0,3).
∵抛物线的对称轴为x=-
| b |
| 2a |
∴D(2,3).
把y=0代入抛物线的解析式得:0=-x2+2x+3,解得x=3或x=-1,
∴A(-1,0).
设直线AD的解析式为y=kx+b,将点A和点D的坐标代入得:
|
∴直线AD的解析式为y=x+1.
(2)如图1所示:

∵直线AD的解析式为y=x+1,
∴∠DAB=45°.
∵EF∥x轴,EG∥y轴,
∴∠GEF=90°,∠GFE=∠DAB=45°
∴△EFG是等腰直角三角形.
∴△EFG的周长=EF+FG+EG=(2+
| 2 |
依题意,设E(t,-t2+2t+3),则G(t,t+1).
∴EG=-t2+2t+3-(t+1)=-(t-
| 1 |
| 2 |
| 9 |
| 4 |
∴EG的最大值为
| 9 |
| 4 |
∴△EFG的周长的最大值为
| 9 |
| 2 |
9
| ||
| 4 |
(3)存在.
①以AD为平行四边形的边时,PQ∥AD,PQ=AD.
∵A,D两点间的水平距离为3,
∴P,Q两点间的水平距离也为3.
∴点Q的横坐标为3或-3.
将x=3和x=-3分别代入y=-x2+2x+3得y=0或y=-12.
∴Q(3,0)或(-3,-12).
②当AD为平行四边形的对角线时,设AD的中点为M,
∵A(-1,0),D(2,3),M为AD的中点,
∴M(
| 1 |
| 2 |
| 3 |
| 2 |
设点Q的横坐标为x,则
| x+0 |
| 2 |
| 1 |
| 2 |
∴点Q的横坐标为1.
将x=1代入y=-x2+2x+3得y=4.
∴这时点Q的坐标为(1,4).
综上所述,当点Q的坐标为Q(3,0)或(-3,-12)或(1,4)时,以A,D,P,Q为顶点的四边形是平行四边形.
看了 如图,已知抛物线y=-x2+...的网友还看了以下:
如图所示,正比例函数y=ax的图像与反比例函数y=k/x的图像交于点A(3,2)M(m,n)是反比 2020-04-08 …
A.互不相交B.允许相交C.允许叶结点相交D.允许树枝结点相交 2020-05-26 …
如图,已知正比例函数y=ax(a不等于0)的图像与反比例函数y=k/x(k不等于0)的图像交于点A 2020-06-27 …
如图二次函数的图象与x轴相交于A、B两点,与y轴相交于C点,点C、D是二次函数图象上的一对对称点, 2020-07-20 …
如图,过y轴上一点A(0,1)作AC平行于x轴,交抛物线如图,过y轴上一点A(0,1)作AC平行X 2020-07-29 …
如图抛物线y=1/4x^2+bx+c与x轴交于A(-2,0)如图抛物线y=1/4x^2+bx+c与 2020-07-29 …
如图,二次函数y=-ax2+2ax+c(a>0)的图象交x轴于A,B两点,交y轴于点C,过A的直线 2020-08-02 …
(2014•龙东地区)如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C( 2020-12-08 …
如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二 2020-12-08 …
一次函数的图像分别与x轴,y轴交与点A,B两点,与反比例函数交于点C,D一次函数的图象与X轴、Y轴分 2021-01-10 …