早教吧作业答案频道 -->数学-->
在等边△ABC中,(1)如图1,P,Q是BC边上的两点,AP=AQ,∠BAP=20°,求∠AQB的度数;(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,
题目详情
在等边△ABC中,
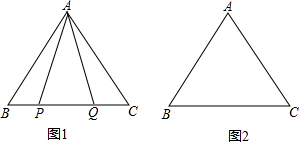
(1)如图1,P,Q是BC边上的两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②小茹通过观察、实验提出猜想:在点P,Q运动的过程中,始终有PA=PM,小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明PA=PM,只需证△APM是等边三角形;
想法2:在BA上取一点N,使得BN=BP,要证明PA=PM,只需证△ANP≌△PCM;
想法3:将线段BP绕点B顺时针旋转60°,得到线段BK,要证PA=PM,只需证PA=CK,PM=CK…
请你参考上面的想法,帮助小茹证明PA=PM(一种方法即可).

(1)如图1,P,Q是BC边上的两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②小茹通过观察、实验提出猜想:在点P,Q运动的过程中,始终有PA=PM,小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明PA=PM,只需证△APM是等边三角形;
想法2:在BA上取一点N,使得BN=BP,要证明PA=PM,只需证△ANP≌△PCM;
想法3:将线段BP绕点B顺时针旋转60°,得到线段BK,要证PA=PM,只需证PA=CK,PM=CK…
请你参考上面的想法,帮助小茹证明PA=PM(一种方法即可).
▼优质解答
答案和解析
(1)∵AP=AQ,
∴∠APQ=∠AQP,
∴∠APB=∠AQC,
∵△ABC是等边三角形,
∴∠B=∠C=60°,
∴∠BAP=∠CAQ=20°,
∴∠AQB=∠APQ=∠BAP+∠B=80°;
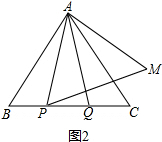 (2)如图2,∵AP=AQ,
(2)如图2,∵AP=AQ,
∴∠APQ=∠AQP,
∴∠APB=∠AQC,
∵△ABC是等边三角形,
∴∠B=∠C=60°,
∴∠BAP=∠CAQ,
∵点Q关于直线AC的对称点为M,
∴AQ=AM,∠QAC=∠MAC,
∴∠MAC=∠BAP,
∴∠BAP+∠PAC=∠MAC+∠CAP=60°,
∴∠PAM=60°,
∵AP=AQ,
∴AP=AM,
∴△APM是等边三角形,
∴AP=PM.
∴∠APQ=∠AQP,
∴∠APB=∠AQC,
∵△ABC是等边三角形,
∴∠B=∠C=60°,
∴∠BAP=∠CAQ=20°,
∴∠AQB=∠APQ=∠BAP+∠B=80°;
 (2)如图2,∵AP=AQ,
(2)如图2,∵AP=AQ,∴∠APQ=∠AQP,
∴∠APB=∠AQC,
∵△ABC是等边三角形,
∴∠B=∠C=60°,
∴∠BAP=∠CAQ,
∵点Q关于直线AC的对称点为M,
∴AQ=AM,∠QAC=∠MAC,
∴∠MAC=∠BAP,
∴∠BAP+∠PAC=∠MAC+∠CAP=60°,
∴∠PAM=60°,
∵AP=AQ,
∴AP=AM,
∴△APM是等边三角形,
∴AP=PM.
看了 在等边△ABC中,(1)如图...的网友还看了以下:
已知曲线C:y=-x^2+x+2与曲线C'关于点P(a,2a)中心对称,并且C与C’相交与A、B两 2020-04-05 …
设圆柱的高为6,底面半径为R,底面周长为C.圆柱的体积为V:写出C关于R,V关于R,V关于C的函数 2020-05-13 …
已知集合A属于B(那个符号打不上去),B={X|X=K/4+1/2,K∈Z}C={X|X=K/8+ 2020-05-13 …
已知A={第一象限角},B={锐角},C={小于90°的角},那么A、B、C关系是()A.B∪C= 2020-05-14 …
已知A={第一象限角},B={锐角},C={小于90°的角},那么A、B、C关系是什么 2020-05-16 …
已知A={第一象限角},B={锐角},C={小于90°的角},那么A、B、C关系是( )A.B=A 2020-05-16 …
设a,b,c都是正数,且3^a=4^b=6^c,求a,b,c关系是2/c=2/a+1/b 2020-06-03 …
离散数学中的复合关系.因为是自学的,基础不好.有一个看不懂设R是由A={1,2,3,4}到B={2 2020-06-28 …
设圆柱的高为6cm,底面半径为rcm,底面周长为Ccm,圆柱的体积为Vcm3.(1)分别写出C关于 2020-06-30 …
生活垃圾无害化处理的方法之一是垃圾发电技术的应用,下列说法正确的是()A.生活垃圾焚烧处理后体积一 2020-07-01 …