早教吧作业答案频道 -->数学-->
已知如图半圆O的半径OA=4,P是OA延长线上一点,过线段OP的中点B作垂线交O于点C,射线PC交O于点D,联结OD.(1)若AC=CD,求∠COD的度数;(2)若AC=CD,求弦CD的长;(3)若点C在AD上时,设PA=
题目详情
已知如图半圆O的半径OA=4,P是OA延长线上一点,过线段OP的中点B作垂线交 O于点C,射线PC交 O于点D,联结OD.
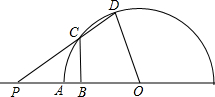
(1)若
=
,求∠COD的度数;
(2)若
=
,求弦CD的长;
(3)若点C在
上时,设PA=x,CD=y,求y与x的函数关系式及自变量x的取值范围.

(1)若
 |
| AC |
 |
| CD |
(2)若
 |
| AC |
 |
| CD |
(3)若点C在
 |
| AD |
▼优质解答
答案和解析
(1)连接OC,如图1,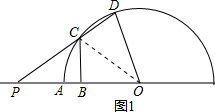
∵BC⊥PO,PB=OB,
∴CP=CO,
∴∠P=∠COP,
∵
=
,
∴∠DOC=∠COP,
在△COD中,2∠DCO+∠DOC=180°,
∵∠DCO=∠P+∠COP=2∠COP=2∠DOC,
∴5∠DOC=180°,
∴∠DOC=36°;
(2)∵
=
,
∴∠DOC=∠COP,
∵BC垂直平分OP,
∴PC=OC=4,
∴∠P=∠POC=∠DOC,
∴△DOC∽△DPO,
∴
=
,
设CD=y,则16=(y+4)y,解得:y=2
-2,
即CD的长为2
-2;
(3)延长PO交圆于Q点,连结AC,如图2,
∵∠PQD+∠ACD=180°,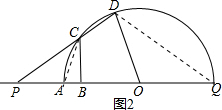
∴∠PCA=∠PQD,
∵∠P=∠P,
∴△PCA∽△PQD,
∴
=
,
∴4(4+y)=x(x+8),
∴y=
(4
-4<x<4).

∵BC⊥PO,PB=OB,
∴CP=CO,
∴∠P=∠COP,
∵
 |
| AC |
 |
| CD |
∴∠DOC=∠COP,
在△COD中,2∠DCO+∠DOC=180°,
∵∠DCO=∠P+∠COP=2∠COP=2∠DOC,
∴5∠DOC=180°,
∴∠DOC=36°;
(2)∵
 |
| AC |
 |
| CD |
∴∠DOC=∠COP,
∵BC垂直平分OP,
∴PC=OC=4,
∴∠P=∠POC=∠DOC,
∴△DOC∽△DPO,
∴
| DO |
| DP |
| DC |
| DO |
设CD=y,则16=(y+4)y,解得:y=2
| 5 |
即CD的长为2
| 5 |
(3)延长PO交圆于Q点,连结AC,如图2,
∵∠PQD+∠ACD=180°,

∴∠PCA=∠PQD,
∵∠P=∠P,
∴△PCA∽△PQD,
∴
| PC |
| PQ |
| PA |
| PD |
∴4(4+y)=x(x+8),
∴y=
| x2+8x-16 |
| 4 |
| 2 |
看了 已知如图半圆O的半径OA=4...的网友还看了以下:
如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在C、D之间有一点P,如果P点在C 2020-06-04 …
窦性P波时P波一定直立的导联是( )A.Ⅱ导联B.Ⅲ导联C.aVR导联D.V导联E.V导联 2020-06-07 …
窦性P波时P波一定倒置的导联是( )A.Ⅱ导联B.Ⅲ导联C.aVR导联D.V导联E.V导联 2020-06-07 …
已知互不相等的正数a,b,c,d,p,q满足a,c,b,d成等差数列,a,p,b,q成等比数列,则 2020-06-12 …
已知事件A、B、C、D相互独立,且P(A)=P(B)=P(C)/2=P(D)/2,P(A+B+C+ 2020-06-12 …
设一组初始记录关键字序列为(Q,H,C,Y,P,A,M,S,R,D,F,X),则按字母升序的第一趟 2020-07-17 …
设A、B、C为事件,P(ABC)>0,如果P(AB|C)=P(A|C)P(B|C),则()A.P( 2020-07-20 …
已知平面上的曲线C及点P,在C上任取一点Q,定义线段PQ长度的最小值为点P到曲线C的距离,记作d( 2020-07-30 …
S²=(p-a)(p-b)(p-c)(p-d),其中p=½(a+b+c+d)这个公式怎么用S²=(p 2020-11-07 …
7,如果事件ABC相互独立,则下列等式中正确的是()A,P(A+B+C)=P(A)+P(B)+P(C 2020-12-01 …