早教吧作业答案频道 -->数学-->
已知正方形ABCD如图所示,连接其对角线AC,∠DAC的平分线AE交CD于点E,过点D作DM⊥AE于F,交AC于点M,共过点A作AN⊥AE交CB延长线于点N.(1)若AD=3,求△CAN的面积;(2)求证:AN=DM+2EF.
题目详情
已知正方形ABCD如图所示,连接其对角线AC,∠DAC的平分线AE交CD于点E,过点D作DM⊥AE于F,交AC于点M,共过点A作AN⊥AE交CB延长线于点N.
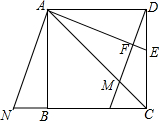
(1)若AD=3,求△CAN的面积;
(2)求证:AN=DM+2EF.

(1)若AD=3,求△CAN的面积;
(2)求证:AN=DM+2EF.
▼优质解答
答案和解析
(1) ∵四边形ABCD是正方形,
∴AD=AB=BC=CD=3,∠DAB=∠ABC=∠BCD=∠DC=90°,∠CAB=∠CAD=∠ACB=45°,
∵AE平分∠DAC,
∴∠DAE=∠EAC=22.5°,
∵AE⊥AN,
∴∠NAE=90°,∠NAC=90°-∠CAE=67.5°,∠N=180°-∠NAC-∠CN=67.5°,
∴∠N=∠NAC
∴CA=CN=
=
=3
,
∴S△ACN=
×CN×AB=
×3
×3=
.
(2)在FA上截取FH=FE,连接DH.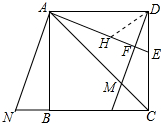
∵AE⊥DM,
∴DH=DE,
∴∠DHE=∠DEH=90°-∠DAE=67.5°,
∴∠MDC=∠HDF=90°-∠DEA=22.5°,
∴∠ADH=90°-∠HDE=45°,
∴∠ADH=∠MCD,∠DAH=∠MDC,
在△ADH和△DCM中,
,
∴△ADH≌△DCM,
∴AH=DM,
在△ABN和△ADE中,
,
∴△ABN≌△ADE,
∴AN=AE,
∴AN=AH+HE=DM+2EF.
∴AD=AB=BC=CD=3,∠DAB=∠ABC=∠BCD=∠DC=90°,∠CAB=∠CAD=∠ACB=45°,
∵AE平分∠DAC,
∴∠DAE=∠EAC=22.5°,
∵AE⊥AN,
∴∠NAE=90°,∠NAC=90°-∠CAE=67.5°,∠N=180°-∠NAC-∠CN=67.5°,
∴∠N=∠NAC
∴CA=CN=
| AB2+BC2 |
| 32+32 |
| 2 |
∴S△ACN=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
9
| ||
| 2 |
(2)在FA上截取FH=FE,连接DH.

∵AE⊥DM,
∴DH=DE,
∴∠DHE=∠DEH=90°-∠DAE=67.5°,
∴∠MDC=∠HDF=90°-∠DEA=22.5°,
∴∠ADH=90°-∠HDE=45°,
∴∠ADH=∠MCD,∠DAH=∠MDC,
在△ADH和△DCM中,
|
∴△ADH≌△DCM,
∴AH=DM,
在△ABN和△ADE中,
|
∴△ABN≌△ADE,
∴AN=AE,
∴AN=AH+HE=DM+2EF.
看了 已知正方形ABCD如图所示,...的网友还看了以下:
设在关系模式R(A,B,C,D,E,F,G)中,根据语义有如下函数依赖集F={A→B,C→D,C→F 2020-05-23 …
设在关系模式R(A,B,C,D,E,F,G)中,根据语义有如下函数依赖集F=(A→B,C→D,C→F 2020-05-23 …
设在关系模式R(A,B,C,D,E,F,G)中,根据语义有如下函数依赖集F=(A→B,C→D,C→F 2020-05-23 …
设有关系模式R(A,B,C,D,E,F,G),根据语义有如下函数依赖集F={A→B,C→D,C→F, 2020-05-23 …
设有关系模式r(a,b,c,d),f是r上成立的fd集,f={a→d,c→d},则相对于f,关系模式 2020-05-26 …
设给定关系模式R(U,F)其中U={A,B,C,D,E},F={A→D,E→D,D→B,BC→D, 2020-07-01 …
立体几何截面立方体abcd-a'b'c'd',ab上有一点e,cc'上有一点f,a'd'上有一点g 2020-07-20 …
设函数f(x)在[a,b]上连续,在(a,b)上可导且f'(x)≠0那么下列一定成立的是()A.f( 2020-11-03 …
原函数积分加反函数积分…我总不可能画个图吧…怎办…原函数f(x)在[a,b]上单调递增,a>0,f( 2020-11-08 …
下列结论正确命题的序号是()A.∫baf(x)dx=ni=1f(ξ)b−anB.∫baf(x)dx= 2020-12-23 …