早教吧作业答案频道 -->数学-->
已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.(1)求证:BD是⊙O的切线;(2)求证:CE2=EH•EA;(3)若⊙O
题目详情
已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
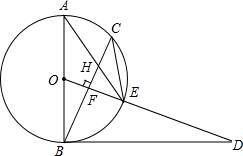
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EH•EA;
(3)若⊙O的半径为
,sinA=
,求BH的长.

(1)求证:BD是⊙O的切线;
(2)求证:CE2=EH•EA;
(3)若⊙O的半径为
| 5 |
| 2 |
| 3 |
| 5 |
▼优质解答
答案和解析
(1)证明:如图1中,
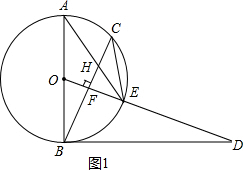
∵∠ODB=∠AEC,∠AEC=∠ABC,
∴∠ODB=∠ABC,
∵OF⊥BC,
∴∠BFD=90°,
∴∠ODB+∠DBF=90°,
∴∠ABC+∠DBF=90°,
即∠OBD=90°,
∴BD⊥OB,
∴BD是⊙O的切线;
(2)证明:连接AC,如图2所示:
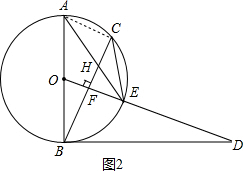
∵OF⊥BC,
∴
=
,
∴∠CAE=∠ECB,
∵∠CEA=∠HEC,
∴△CEH∽△AEC,
∴
=
,
∴CE2=EH•EA;
(3) 连接BE,如图3所示:
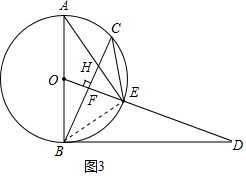
∵AB是⊙O的直径,
∴∠AEB=90°,
∵⊙O的半径为
,sin∠BAE=
,
∴AB=5,BE=AB•sin∠BAE=5×
=3,
∴EA=
=4,
∵
=
,
∴BE=CE=3,
∵CE2=EH•EA,
∴EH=
,
∴在Rt△BEH中,BH=
=
=
.

∵∠ODB=∠AEC,∠AEC=∠ABC,
∴∠ODB=∠ABC,
∵OF⊥BC,
∴∠BFD=90°,
∴∠ODB+∠DBF=90°,
∴∠ABC+∠DBF=90°,
即∠OBD=90°,
∴BD⊥OB,
∴BD是⊙O的切线;
(2)证明:连接AC,如图2所示:

∵OF⊥BC,
∴
 |
| BE |
 |
| CE |
∴∠CAE=∠ECB,
∵∠CEA=∠HEC,
∴△CEH∽△AEC,
∴
| CE |
| EH |
| EA |
| CE |
∴CE2=EH•EA;
(3) 连接BE,如图3所示:

∵AB是⊙O的直径,
∴∠AEB=90°,
∵⊙O的半径为
| 5 |
| 2 |
| 3 |
| 5 |
∴AB=5,BE=AB•sin∠BAE=5×
| 3 |
| 5 |
∴EA=
| AB2-BE2 |
∵
 |
| BE |
 |
| CE |
∴BE=CE=3,
∵CE2=EH•EA,
∴EH=
| 9 |
| 4 |
∴在Rt△BEH中,BH=
| BE2+EH2 |
32+(
|
| 15 |
| 4 |
看了 已知,如图,AB是⊙O的直径...的网友还看了以下:
如图,∠A=90°,E为BC上一点,A点和E点关于BD对称,B点、C点关于DE对称,求∠ABC和∠ 2020-04-11 …
下图中AB、CD为两条纬线,B、C、E位于同一经线上,A、E、D为晨昏线上的三点,此时太阳高度为0 2020-04-27 …
有关方向的判断,正确的是()A、A点位于B点的西北方向B、C点位于E点的正东方向C、C点位于D点的 2020-05-13 …
如图,AB为⊙O的直径,CD⊥AB于点E,交⊙O于点D,OF⊥AC于点F.当∠D=30°,BC=1 2020-05-15 …
已知,如图,△ABC中,AB=BC,D是AC中点,BE平分∠ABD交AC于点E,点O是AB上一点, 2020-06-13 …
答对再+100分!已知一个二次函数的图像经过点A(—1,0),B(0,3),C(4,-5).(1) 2020-06-13 …
如图,在Rt三角形ABC中,角C=90度,AE平分角BAC交BC于E,点O在AB上,以OA为半径的 2020-06-27 …
△ABC内接于⊙O,I是△ABC的内心,AI的延长线交BC于点E,交⊙O于点D,连接BD.(1)求 2020-07-31 …
△ABC内接于⊙O,I是△ABC的内心,AI的延长线交BC于点E,交⊙O于点D,连接BD.(1)求 2020-07-31 …
△ABC内接于⊙O,BC为⊙O直径,∠ACB=60°,AD为∠BAC的平分线交⊙O于D,BE⊥AD于 2021-02-04 …