早教吧作业答案频道 -->数学-->
正方形ABCD中,M,N分别是CB,DC延长线上的一点,且有DN-BM=MN.(1)求证:∠MAN=45°.(2)过点D作DP⊥AN交AM于P,连CP,求线段PA,PC,PD之间的数量关系.(3)若点C为DN的中点,且AB=1,求CP的
题目详情
正方形ABCD中,M,N分别是CB,DC延长线上的一点,且有DN-BM=MN.
(1)求证:∠MAN=45°.
(2)过点D作DP⊥AN交AM于P,连CP,求线段PA,PC,PD之间的数量关系.
(3)若点C为DN的中点,且AB=1,求CP的长.
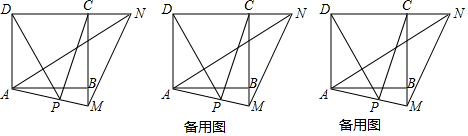
(1)求证:∠MAN=45°.
(2)过点D作DP⊥AN交AM于P,连CP,求线段PA,PC,PD之间的数量关系.
(3)若点C为DN的中点,且AB=1,求CP的长.

▼优质解答
答案和解析
(1)证明:如图1中,作AH⊥AM交CD于H.
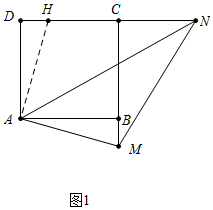
∵∠HAB=∠DAB=90°,
∴∠DAH=∠BAM,
∵∠D=∠ABM=90°,AD=AB,
∴△ADH≌△ABM,
∴DH=BM,AH=AM,
∵DN-BM=MN,
∴DN-DH=MN
∴HN=MN,∵AN=AN,
∴△ANH≌△ANM,
∴∠NAM=∠NAH=45°.
(2) 结论:PA+PC=
PD.
理由:如图2中,作DQ⊥PC于Q,DG⊥PA于G,PD交AC于O,交AN于T.
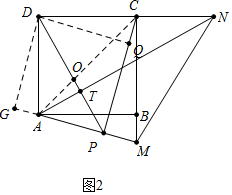
∵PD⊥AN,
∴∠ATP=90°,∵∠PAT=45°,
∴∠APO=∠DCO=45°,∵∠DOC=∠AOP,
∴△DOC∽△AOP,
∴
=
,
∴
=
,∵∠DOA=∠POC,
∴△DOA∽△COP,
∴∠CPD=∠DAO=45°,
∴∠DPA=∠DPC,
∵PD=PD,∠G=∠PQD=90°,
∴△PDO≌△PDQ,
∴DG=DQ,PG=PQ,
易证△ADG≌△CDQ,四边形PQDG是正方形,
∴AQ=CQ,
∴PA+PC=(PG-AG)+(PQ+CQ)=2PG,
∵PD=
PG,
∴PA+PC=
PD.
(3) 如图3中,连接AC.
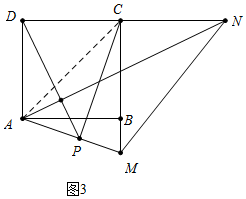
由(2)可知DN-BM=MN,设BM=x则MN=2-x,
在Rt△CMN中,∵CM2+CN2=MN2,
∴(x+1)2+12=(2-x)2,
∴x=
,
由(2)可知PC⊥AM,
∴
•AM•PC=
•CM•AB,
∴PC=
=
.

∵∠HAB=∠DAB=90°,
∴∠DAH=∠BAM,
∵∠D=∠ABM=90°,AD=AB,
∴△ADH≌△ABM,
∴DH=BM,AH=AM,
∵DN-BM=MN,
∴DN-DH=MN
∴HN=MN,∵AN=AN,
∴△ANH≌△ANM,
∴∠NAM=∠NAH=45°.
(2) 结论:PA+PC=
| 2 |
理由:如图2中,作DQ⊥PC于Q,DG⊥PA于G,PD交AC于O,交AN于T.

∵PD⊥AN,
∴∠ATP=90°,∵∠PAT=45°,
∴∠APO=∠DCO=45°,∵∠DOC=∠AOP,
∴△DOC∽△AOP,
∴
| DO |
| AO |
| OC |
| OP |
∴
| DO |
| OC |
| AO |
| OP |
∴△DOA∽△COP,
∴∠CPD=∠DAO=45°,
∴∠DPA=∠DPC,
∵PD=PD,∠G=∠PQD=90°,
∴△PDO≌△PDQ,
∴DG=DQ,PG=PQ,
易证△ADG≌△CDQ,四边形PQDG是正方形,
∴AQ=CQ,
∴PA+PC=(PG-AG)+(PQ+CQ)=2PG,
∵PD=
| 2 |
∴PA+PC=
| 2 |
(3) 如图3中,连接AC.

由(2)可知DN-BM=MN,设BM=x则MN=2-x,
在Rt△CMN中,∵CM2+CN2=MN2,
∴(x+1)2+12=(2-x)2,
∴x=
| 1 |
| 3 |
由(2)可知PC⊥AM,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴PC=
1×
| ||||
|
2
| ||
| 5 |
看了 正方形ABCD中,M,N分别...的网友还看了以下:
如图所示,正比例函数y=ax的图像与反比例函数y=k/x的图像交于点A(3,2)M(m,n)是反比 2020-04-08 …
在直角坐标系中,M为x轴正半轴上一点,⊙M交x轴于A、B两点,交y轴于C、D两点,P为AB延长线上 2020-05-17 …
(2006•永春县)函数y=-x+4与x轴交于点A,与y轴交于点B,动点M在x轴的正半轴上,N为O 2020-06-14 …
痛苦和欢乐,生活和梦幻,摆脱与追求,都在这舞姿和鼓点中,交织!旋转!凝聚!奔突!辐射!翻飞!升华! 2020-07-09 …
如图在平面直角坐标系中,M为x轴上一点,⊙M交x轴于A、B两点,交y轴于C、D两点,P为BC上的一 2020-07-30 …
平面直角坐标系中,O是坐标原点,点A是第一象限内一点,A(m,n)满足2m-n=10m-2n=-4 2020-08-01 …
已知点M(a,b)(ab≠0)是圆x2+y2=r2内一点,直线m是以点M为中点的弦所在的直线,直线l 2020-11-02 …
如图已知函数y=-1/2x+b的图像与x轴y轴分别交于点A、B与函数y=x的图像交于点M点M的如图已 2020-12-12 …
十万火急!仿写(按照例句写一段描写狂风暴雨的话)例句:痛苦和欢乐,生活和梦幻,摆脱和追求,都在这舞姿 2020-12-14 …
如图,平面直角坐标系中,A(-3,1)B(-1,4)1.求S△AOB2.直线AB交X轴于M点如图,平 2021-01-10 …