平面直角坐标系中，O是坐标原点，点A是第一象限内一点，A（m，n）满足2m-n=10m-2n=-4过点A分别作x轴和y轴的平行线，交y轴于点B，交x轴于点C．M是线段AB的中点，点P从M点出发沿线段MA-AC向终点C

Question

平面直角坐标系中，O是坐标原点，点A是第一象限内一点，A（m，n）满足

2m-n=10

m-2n=-4

过点A分别作x轴和y轴的平行线，交y轴于点B，交x轴于点C．M是线段AB的中点，点P从M点出发沿线段MA-AC向终点C运动，速度为每秒2个单位长度．设点P运动的时间为t（秒）．

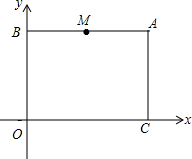
（1）求出A点坐标．
（2）用含有t的代数式表示线段AP的长度．
（3）作线段OP、PM、OM，当三角形MOP的面积等于直角梯形AMOC的面积的(1)/(2)时，求t的值，并求出此时点P的坐标．

Answer 1

（1）解方程组

2m-n=10

m-2n=-4

得：

m=8

n=6

，
即A的坐标为（8，6）；

（2）∵根据题意知：四边形OBAC是矩形，A（8，6），M为AB的中点，
∴OB=AC=6，AB=OC=8，AM=BM=4，
当P在MA上时，AP=4-2t；
当P在AC上时，AP=2t-4；

（3）
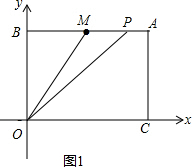
当P在AM上时，如图1，
∵当三角形MOP的面积等于直角梯形AMOC的面积的(1)/(2)，
∴(1)/(2)•2t•6=(1)/(2)×(1)/(2)×（4+8）×6，
解得：t=3，当t=3时，MP=6>AM，此时不符合P在AM上，舍去；
当P在AC上时，如图2，

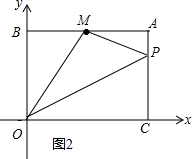
∵S_△OMP=S_{四边形AMOC}-S_△AMP-S_△OPC=(1)/(2)×（4+8）×6-(1)/(2)×4×（2t-4）-(1)/(2)×（4+6-2t）×8=4+4t，
S_{四边形AMOC}=(1)/(2)×（4+8）×6=36，
∴4+4t=(1)/(2)×36，
解得：t=(7)/(2)，
AP=2t-4=3，CP=6-3=3，
P点的坐标为（8，3）．