早教吧作业答案频道 -->数学-->
正△ABC的边长为2,M是AB边上的中点,P是BC边上的任意一点,PA+PM的最大值是,最小值是.
题目详情
正△ABC的边长为2,M是AB边上的中点,P是BC边上的任意一点,PA+PM的最大值是___,最小值是___.
▼优质解答
答案和解析
如图1所示:作点M关于CB的对称点M′连接AM′、M′C.
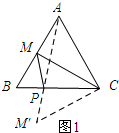
∵点M与点M′关于BC对称,
∴MP=M′P,∠MCP=∠M′CP.
∵△ABC是正三角形,M是AB的中点,
∴MC=CM′,∠MCP=∠ACP=30°.
∴∠MCP=∠ACP=∠M′CP=30°.
∴CM′=MC=BC×cos30°=2×
=
.
∴∠ACM′=90°.
∴AM′=
=
.
∴PA+PM的最小值是
.
如图2所示:当点P与点C重合时.PM+PA有最大值.
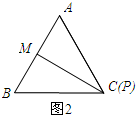
∵PM=
,AP=2,
∴PA+PM=2+
.
故答案为:2+
;
.

∵点M与点M′关于BC对称,
∴MP=M′P,∠MCP=∠M′CP.
∵△ABC是正三角形,M是AB的中点,
∴MC=CM′,∠MCP=∠ACP=30°.
∴∠MCP=∠ACP=∠M′CP=30°.
∴CM′=MC=BC×cos30°=2×
| ||
| 2 |
| 3 |
∴∠ACM′=90°.
∴AM′=
| AM2+M′C2 |
| 7 |
∴PA+PM的最小值是
| 7 |
如图2所示:当点P与点C重合时.PM+PA有最大值.

∵PM=
| 3 |
∴PA+PM=2+
| 3 |
故答案为:2+
| 3 |
| 7 |
看了 正△ABC的边长为2,M是A...的网友还看了以下:
有一边长为q的正方形abcd,p是在对角线BD上的一点,p点在什么位置时ap+bp+cp的值最小. 2020-04-27 …
(1)如图2,四边形ABCD是边长为20的菱形,且∠DAB=60°,P是线段AC上的动点,E在AB 2020-05-13 …
小明、小亮、小梅、小花四人共同探讨代数式x2-6x+10的值的情况.他们作了如下分工:小明负责找其 2020-05-17 …
在20:如图8,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知 2020-05-21 …
若某一次函数,当x的值减小1,y的值就减小2,那么x的值减小2时,y的值不好意思,题答错了应该是若 2020-06-14 …
小聪、小明、小伶、小俐四人共同探究代数式2x2-4x+6的值的情况.他们作了如下分工:小聪负责找值 2020-07-12 …
小明、小亮、小梅、小花四人共同探究代数式的值的情况.他们作了如下分工:小聪负责找值为0时x的值,小 2020-07-12 …
小聪、小明、小伶、小俐四人共同探究代数式2x2-4x+6的值的情况.他们作了如下分工:小聪负责找值 2020-07-12 …
如图,点E是正方形ABCD的边DC上的一点,在AC上找一点P,使PD+PE的值最小,这个最小值等于 2020-07-21 …
如图,菱形ABCD的边长为2cm,∠A=120°,点E是BC边上的动点,点P是对角线BD上的动点, 2020-07-21 …