在平面直角坐标系中，点A（-2a，a-1）在x轴上，将点A向右平移5个单位长度，向上平移m（m>2）个单位长度，得到点B，直线l是平行于x轴，纵坐标都是1的直线，点C与点B关于直线l轴对称．（

Question

在平面直角坐标系中，点A（-2a，a-1）在x轴上，将点A向右平移5个单位长度，向上平移m（m>2）个单位长度，得到点B，直线l是平行于x轴，纵坐标都是1的直线，点C与点B关于直线l轴对称．

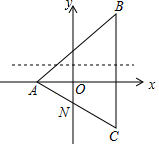
（1）写出点A，B，C的坐标（可用含m的式子表示）；
（2）若S_△ABC=10，求m的值；
（3）若AC交y轴于N，ON=1，求m的值．

Answer 1

（1）∵点A（-2a，a-1）在x轴上，
∴a-1=0，解得：a=1，
∴-2a=-2，
∴点A（-2，0）．
∵将点A向右平移5个单位长度，向上平移m（m>2）个单位长度，得到点B，
∴点B（3，m）．
∵点C与点B关于直线l：y=1轴对称，
∴点C（3，2-m）．
（2）∵B（3，m），C（3，2-m），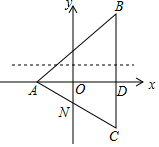
∴BC=2m-2，
∴S_△ABC=(1)/(2)×5BC=5m-5=10，
解得：m=3．
（3）设BC与x轴的交点为点D，则△AON∽△ADC，如图所示．
∵△AON∽△ADC，
∴(AO)/(AD)=(ON)/(DC)，即(2)/(5)=(1)/(m-2)，
解得：m=(9)/(2)，
经检验，m=(9)/(2)是原分式方程的解．