早教吧作业答案频道 -->数学-->
如图,在△ABC中,AB=AC=5,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且sinα=35.下列结论:①△ADE∽△ACD;②当BD=2时,△ABD与△DCE全等;③△DCE为直
题目详情
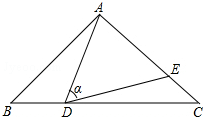
如图,在△ABC中,AB=AC=5,点D是边BC上一动点(不与B,C重合),
∠ADE=∠B=α,DE交AC于点E,且sinα=
.下列结论:
①△ADE∽△ACD;
②当BD=2时,△ABD与△DCE全等;
③△DCE为直角三角形时,BD的长一定为4;
④0<CE≤3.2.
其中正确的结论是___.(把你认为正确结论的序号都填上)
∠ADE=∠B=α,DE交AC于点E,且sinα=
| 3 |
| 5 |
①△ADE∽△ACD;
②当BD=2时,△ABD与△DCE全等;
③△DCE为直角三角形时,BD的长一定为4;
④0<CE≤3.2.
其中正确的结论是___.(把你认为正确结论的序号都填上)

▼优质解答
答案和解析
①∵AB=AC,
∴∠B=∠C,
又∵∠ADE=∠B
∴∠ADE=∠C,
∴△ADE∽△ACD;
故①正确,
②作AG⊥BC于G,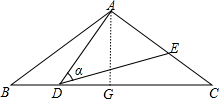
∵AB=AC=5,∠ADE=∠B=α,sinα=
,
∴cosB=cosα=
=
,
∴BG=ABcosB,
∴BC=2BG=2ABcosB=2×5×
=8,
∵BD=2,
∴DC=6,
∴AB≠DC,
∴△ABD与△DCE不全等,故②错误,
③当∠AED=90°时,由①可知:△ADE∽△ACD,
∴∠ADC=∠AED,
∵∠AED=90°,
∴∠ADC=90°,
即AD⊥BC,
∵AB=AC,
∴BD=CD,
∴∠ADE=∠B=α且cosα=
,AB=5,
∴BD=4,
当∠CDE=90°时,易△CDE∽△BAD,
∵∠CDE=90°,
∴∠BAD=90°,
∵∠B=α且cosα=
,AB=5,
∴cosB=
=
,
∴BD=
.
故③错误.
∵AG⊥BC于G,如图,
∵AB=AC,
∴BG=CG,
∵∠ADE=∠B=α,
∴cosB=cosα=
=
,
∴BG=
×5=4,
∴BC=2BG=8,
设BD=x,则CD=8-x,
∵∠ADC=∠B+∠BAD,即α+∠CDE=∠B+∠BAD,
∴∠CDE=∠BAD,
而∠B=∠C,
∴△ABD∽△DCE,
∴
=
,即
=
,
∴CE=-
x2+
x
=-
(x-4)2+3.2,
当x=4时,CE最大,最大值为3.2.
∴0<CE≤3.2.故④正确.
故答案为:①④.
∴∠B=∠C,
又∵∠ADE=∠B
∴∠ADE=∠C,
∴△ADE∽△ACD;
故①正确,
②作AG⊥BC于G,

∵AB=AC=5,∠ADE=∠B=α,sinα=
| 3 |
| 5 |
∴cosB=cosα=
| 1-sinα |
| 4 |
| 5 |
∴BG=ABcosB,
∴BC=2BG=2ABcosB=2×5×
| 4 |
| 5 |
∵BD=2,
∴DC=6,
∴AB≠DC,
∴△ABD与△DCE不全等,故②错误,
③当∠AED=90°时,由①可知:△ADE∽△ACD,
∴∠ADC=∠AED,
∵∠AED=90°,
∴∠ADC=90°,
即AD⊥BC,
∵AB=AC,
∴BD=CD,
∴∠ADE=∠B=α且cosα=
| 4 |
| 5 |
∴BD=4,
当∠CDE=90°时,易△CDE∽△BAD,
∵∠CDE=90°,
∴∠BAD=90°,
∵∠B=α且cosα=
| 4 |
| 5 |
∴cosB=
| AB |
| BD |
| 4 |
| 5 |
∴BD=
| 25 |
| 4 |
故③错误.
∵AG⊥BC于G,如图,
∵AB=AC,
∴BG=CG,
∵∠ADE=∠B=α,
∴cosB=cosα=
| BG |
| AB |
| 4 |
| 5 |
∴BG=
| 4 |
| 5 |
∴BC=2BG=8,
设BD=x,则CD=8-x,
∵∠ADC=∠B+∠BAD,即α+∠CDE=∠B+∠BAD,
∴∠CDE=∠BAD,
而∠B=∠C,
∴△ABD∽△DCE,
∴
| AB |
| CD |
| BD |
| CE |
| 5 |
| 8-x |
| x |
| CE |
∴CE=-
| 1 |
| 5 |
| 8 |
| 5 |
=-
| 1 |
| 5 |
当x=4时,CE最大,最大值为3.2.
∴0<CE≤3.2.故④正确.
故答案为:①④.
看了 如图,在△ABC中,AB=A...的网友还看了以下:
若a+b=b+c,则a-b(c为整式)若a=b,则ac=bc(c为整式)若ac=bc,则a=b(c 2020-04-22 …
已知实数a,b满足a+b=8,ab=15,且a>b,试求a-b的值解a+b=8,ab=15(a+b 2020-05-17 …
如图正方形被一条曲线分成A、B两部分,下面()说法正确.A.如果a>b,那么A周长大于B周长B.如 2020-05-17 …
2、已知a,b为非零向量,则下列命题中真命题的个数为A若|a|+|b|=|a+b|,则a与b方向相 2020-07-30 …
已知a>0,b>0,则坐标平面上四个点A(a,b),B(a,-b),C.(-a,b),D(-a,- 2020-08-02 …
(a+b+c)^3-(b+c-a)^3-(c+a-b)^3-(a+b-c)^3=[(a+b+c)^ 2020-08-02 …
下面的等量代换怎么做1.A+B=20,B+C=12,C+A=18,ABC各多少2.A+A+A=B+ 2020-08-02 …
数学老师给学生出了一道题,计算:(2(a+b)^5-3(a+b)^4+(-a-b)^3)/(2(a+ 2020-12-09 …
数轴上点A,B所代表的数为a,b,请你计算A,B两点的距离.a=2,b=6,A,B的距离是什么;a- 2020-12-30 …
如果a、b是有理数,则下列各式子成立的是()A.如果a<0,b<0,那么a+b>0B.如果a>0,b 2021-02-02 …