早教吧作业答案频道 -->数学-->
在四棱锥P-ABCD中,四条侧棱长均为2,底面ABCD为正方形,E为PC的中点.若异面直线PA与BE所成的角为45°.则该四锥的体积是.
题目详情
在四棱锥P-ABCD中,四条侧棱长均为2,底面ABCD为正方形,E为PC的中点.若异面直线PA与BE所成的角为45°.则该四锥的体积是___.
▼优质解答
答案和解析
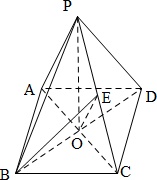 设底面ABCD的中心为O,连结PO,OE,AC,BD,则O是AC的中点,
设底面ABCD的中心为O,连结PO,OE,AC,BD,则O是AC的中点,
∴OE∥PA,OE=
PA=1.∴∠BEO是异面直线PA,BE所成的角,即∠BEO=45°.
∵四棱锥的四条侧棱长均为2,底面ABCD为正方形,
∴PO⊥平面ABCD,OB⊥OC,
∴PO⊥OB,
∴OB⊥平面PAC,∴OB⊥OE.
∴△BOE是等腰直角三角形,∴OB=OE=1.
∴BC=
,PO=
=
.
∴四棱锥的体积V=
×BC2×PO=
×2×
=
.
故答案为
.
 设底面ABCD的中心为O,连结PO,OE,AC,BD,则O是AC的中点,
设底面ABCD的中心为O,连结PO,OE,AC,BD,则O是AC的中点,∴OE∥PA,OE=
| 1 |
| 2 |
∵四棱锥的四条侧棱长均为2,底面ABCD为正方形,
∴PO⊥平面ABCD,OB⊥OC,
∴PO⊥OB,
∴OB⊥平面PAC,∴OB⊥OE.
∴△BOE是等腰直角三角形,∴OB=OE=1.
∴BC=
| 2 |
| PB2-OB2 |
| 3 |
∴四棱锥的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
2
| ||
| 3 |
故答案为
2
| ||
| 3 |
看了 在四棱锥P-ABCD中,四条...的网友还看了以下:
如图,正方体的棱长为ACD分别wie两条棱的中点(1)求四边形ABCD是梯形(2)求四边形ABC如 2020-05-16 …
平行四边形ABCD中,AE和AF分别是BC和CD的高,且三角形AEF是正三角形.(1)求证:四边形 2020-05-17 …
判断下列命题是否正确,并说明理由.(矩形的判定)1、对角互补的平行四边形是矩形.2、一组邻角相等的 2020-05-20 …
#芝麻开门#如图,已知平行四边形ABCD中AC,BD交于点O,E是BD延长线上的点,且△ACE是等 2020-05-23 …
1如图,已知平行四边形的内角平分线AE,BF分别交BC,AD于E,F两点,求证:四边形ABEF是菱 2020-07-06 …
如图,把菱形ABCD沿着BD的方向平移到菱形A/B/C/D/′的位置,(1)求证:重叠部分的四边形 2020-07-15 …
下列说法正确的是:A对顶角互相垂直的四边形是菱角B有一个角是直角的平行四边形是矩形C有一个角是直角 2020-08-01 …
1.梯形ABCD中,AB‖DC,E,F,G,H分别是边AB,BC,CD,DA的中点,梯形ABCD的 2020-08-02 …
1.如果一个正多边形内角等于108度,那么这个多边形是边形?2.如果一个多边形的每个内角都相等,且 2020-08-02 …
1.对角线相等的四边形是矩形.2.三角形不是多边形.3.对角线互相垂直且有一组邻边相等的四边形是菱形 2021-02-01 …