早教吧作业答案频道 -->数学-->
如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:(1)直线DE∥平面A1C1F;(2)平面B1DE⊥平面A1C1F.
题目详情
如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:
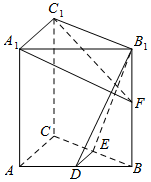
(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.

(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
▼优质解答
答案和解析
(本小题满分14分)
证明:(1)∵D,E为中点,
∴DE为△ABC的中位线,∴DE∥AC,
又∵ABC-A1B1C1为棱柱,
∴AC∥A1C1,∴DE∥A1C1,
又∵A1C1⊂平面A1C1F,且DE⊄A1C1F,
∴DE∥平面A1C1F.…(6分)
(2)∵ABC-A1B1C1为直棱柱,
∴AA1⊥平面A1B1C1,∴AA1⊥A1C1,
又∵A1C1⊥A1B1且AA1∩A1B1=A1,AA1,A1B1⊂平面AA1B1B,
∴A1C1⊥平面AA1B1B,
又A1C1∥AC∥DE,∴DE⊥平面AA1B1B,
又∵A1F⊂平面AA1B1B,∴DE⊥A1F
又∵A1F⊥B1D,DE∩B1D=D,且DE,B1D⊂平面B1DE,
∴A1F⊥平面B1DE,
又∵A1F⊂A1C1F,∴平面B1DE⊥平面A1C1F.…(14分)
证明:(1)∵D,E为中点,

∴DE为△ABC的中位线,∴DE∥AC,
又∵ABC-A1B1C1为棱柱,
∴AC∥A1C1,∴DE∥A1C1,
又∵A1C1⊂平面A1C1F,且DE⊄A1C1F,
∴DE∥平面A1C1F.…(6分)
(2)∵ABC-A1B1C1为直棱柱,
∴AA1⊥平面A1B1C1,∴AA1⊥A1C1,
又∵A1C1⊥A1B1且AA1∩A1B1=A1,AA1,A1B1⊂平面AA1B1B,
∴A1C1⊥平面AA1B1B,
又A1C1∥AC∥DE,∴DE⊥平面AA1B1B,
又∵A1F⊂平面AA1B1B,∴DE⊥A1F
又∵A1F⊥B1D,DE∩B1D=D,且DE,B1D⊂平面B1DE,
∴A1F⊥平面B1DE,
又∵A1F⊂A1C1F,∴平面B1DE⊥平面A1C1F.…(14分)
看了 如图,在直三棱柱ABC-A1...的网友还看了以下:
已知二次函数f(x)=ax^2+bx+c的导数为f'(x),f'(x)>0.对任意实数x,有f(x 2020-05-17 …
已知函数f(x)的定义域为(-1,1),求满足下列条件的实数a的取值范围1.f(x)在定义域内单调 2020-06-02 …
第一题若f(x)=(m-2)x*x+(m+1)x+3在〔1-a,2a]上是偶函数,则m=?,a=? 2020-06-03 …
求详解:函数已知f(x)是定义在R上的奇函数,当0≤x≤1时,f(x)=x²,当x≥0时,f(x+ 2020-06-09 …
改错题:若二次函数f(x)的图像过原点,f(-1):[1,2]f(1):[3,4]求f(-2)范围 2020-06-10 …
已知定义在(1,-1)上的奇函数f(x),在定义域上为减函数,且f(1-a)+f(1-2a)>0, 2020-06-27 …
9.3的a次方=4的b次方=36,问2/a+1/b怎么求出来的(写出过程)10.已知函数f(x)= 2020-07-15 …
设有双射函数f:X->Y,A和B是Y的任意子集,证明:f^-1(A∩B)=f^-1(A)∩f^-1 2020-07-29 …
数学函数几道简答题(1)将F(x)=2^x写成一个奇函数和一个偶函数的和(2)设f(x)是定义在R 2020-08-01 …
①函数Y=X²-mx+2的单调区间为(-无穷,1)则m的取值范围是()②:若f(x+1)=x²-5 2020-08-02 …