早教吧作业答案频道 -->数学-->
如图,三棱柱ABC-A1B1C1中,各棱长均相等,D,E,F分别为棱AB,BC,A1C1的中点.(Ⅰ)证明EF∥平面A1CD;(Ⅱ)若三棱柱ABC-A1B1C1为直棱柱,求直线BC与平面A1CD所成角的正弦值.
题目详情
如图,三棱柱ABC-A1B1C1中,各棱长均相等,D,E,F分别为棱AB,BC,A1C1的中点.
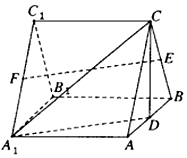
(Ⅰ)证明EF∥平面A1CD;
(Ⅱ)若三棱柱ABC-A1B1C1为直棱柱,求直线BC与平面A1CD所成角的正弦值.

(Ⅰ)证明EF∥平面A1CD;
(Ⅱ)若三棱柱ABC-A1B1C1为直棱柱,求直线BC与平面A1CD所成角的正弦值.
▼优质解答
答案和解析
 证明:(I)连接DE,
证明:(I)连接DE,
∵D,E分别是AB,BC的中点,
∴DE
AC,
∵F是A1C1的中点,∴A1F=
A1C1,
又AC
A1C1,
∴A1F
DE,
∴四边形A1DEF是平行四边形,
∴EF∥A1D,又EF⊄平面A1CD,A1D⊂平面A1CD,
∴EF∥平面A1CD.
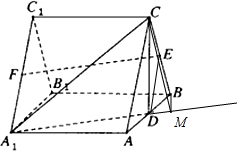
(II)过B作BM⊥A1D交延长线于M,连接CM,
∵ABC是等边三角形,∴CD⊥AB,
又A1A⊥平面ABC,CD⊂平面ABC,
∴A1A⊥CD,
∴CD⊥平面ABCD,又BM⊂平面ABCD,
∴CD⊥BM,又CD⊂平面A1CD,A1D⊂平面A1CD,CD∩A1D=D,
∴BM⊥平面A1CD,
∴∠BCM为直线BC与平面A1CD所成的角,
设直三棱柱棱长为1,则BM=
,
∴sin∠BCM=
=
.
 证明:(I)连接DE,
证明:(I)连接DE,∵D,E分别是AB,BC的中点,
∴DE
| ∥ |
. |
| 1 |
| 2 |
∵F是A1C1的中点,∴A1F=
| 1 |
| 2 |
又AC
| ∥ |
. |
∴A1F
| ∥ |
. |
∴四边形A1DEF是平行四边形,
∴EF∥A1D,又EF⊄平面A1CD,A1D⊂平面A1CD,
∴EF∥平面A1CD.
(II)过B作BM⊥A1D交延长线于M,连接CM,
∵ABC是等边三角形,∴CD⊥AB,
又A1A⊥平面ABC,CD⊂平面ABC,
∴A1A⊥CD,
∴CD⊥平面ABCD,又BM⊂平面ABCD,
∴CD⊥BM,又CD⊂平面A1CD,A1D⊂平面A1CD,CD∩A1D=D,
∴BM⊥平面A1CD,
∴∠BCM为直线BC与平面A1CD所成的角,
设直三棱柱棱长为1,则BM=
| ||
| 5 |
∴sin∠BCM=
| BM |
| BC |
| ||
| 5 |
看了 如图,三棱柱ABC-A1B1...的网友还看了以下:
excel中根据某列的值选择函数中的标准值比如如果A列中的值≥20的,则要求B、C、D、E列值分别 2020-05-13 …
已知函数f(x)=lnx+1/x+ax.其中x>0,常数a∈R.已知函数f(x)=lnx+1/x+ 2020-05-13 …
在物理学内容中,如果某一物体质量为m,它运动时的能量E与它的运动速度v之间的关系(1)若物体质量为 2020-05-16 …
实验室备有下列器材:A.待测定值电阻Rx:阻值在49~52Ω之间B.滑动变阻器:最大阻值见图甲C. 2020-06-30 …
已知函数y=(e^x-a)^2+(e^(-x)-a)^2(a属于R,a不等于0),求y的最小值Y= 2020-07-21 …
编写程序,利用以下公式计算e的值:e≈1+1/1!+1/2!+1/3!+1/4!+1/5!+1/6 2020-08-02 …
对于函数f(x)=ex-x在区间[1,2]上的最值,下列描述正确的是()A.最小值为e-1,没有最大 2020-11-24 …
已知a∈R,函数f(x)=e^x+a|x-2|.(1)当0<a≤e时,若函数f(x)在区间[1,+∞ 2020-12-03 …
∵E=MC^2,∴C=√E/M,又∵M是定值,而E不是定值,∴C不是定值,可以这样说吗?在恒星的原子 2020-12-31 …
已知双曲线x^2/a^2-y^2/b^2=1(a大于0,b大于0)的左、右焦点分别为F1,F2,点P 2020-12-31 …