早教吧作业答案频道 -->数学-->
如图,三角形PCD所在的平面与等腰梯形ABCD所在的平面垂直,AB=AD=12CD,AB∥CD,CP⊥CD,M为PD的中点.(1)求证:AM∥平面PBC;(2)求证:平面BDP⊥平面PBC.
题目详情
如图,三角形PCD所在的平面与等腰梯形ABCD所在的平面垂直,AB=AD=
CD,AB∥CD,CP⊥CD,M为PD的中点.
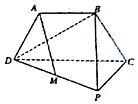
(1)求证:AM∥平面PBC;
(2)求证:平面BDP⊥平面PBC.
| 1 |
| 2 |

(1)求证:AM∥平面PBC;
(2)求证:平面BDP⊥平面PBC.
▼优质解答
答案和解析
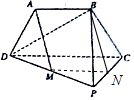 证明:(1)取PC的中点N,连结MN,BN,
证明:(1)取PC的中点N,连结MN,BN,
则MN
CD,又AB
CD,
∴四边形ABNM是平行四边形,
∴AM∥BN,又AM⊄平面PBC,BN⊂平面PBC,
∴AM∥平面PBC.
(2)∵平面ABCD⊥平面PCD,平面ABCD∩平面PCD=CD,CD⊥PC,PC⊂平面PCD,
∴PC⊥平面ABCD,∵BD⊂平面ABCD,
∴BD⊥PC,
∵四边形ABCD是等腰梯形,AD=AB=BC=
CD,
则cos∠BCD=
=
,即∠BCD=60°,
∴BD2=BC2+CD2-BC•CD=3BC2,∴BC2+BD2=CD2,
∴BD⊥BC,
又BC∩PC=C,BC⊂平面PBC,PC⊂平面PBC,
∴BD⊥平面PBC,又BD⊂平面PBD,
∴平面PBD⊥平面PBC.
 证明:(1)取PC的中点N,连结MN,BN,
证明:(1)取PC的中点N,连结MN,BN,则MN
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
∴四边形ABNM是平行四边形,
∴AM∥BN,又AM⊄平面PBC,BN⊂平面PBC,
∴AM∥平面PBC.
(2)∵平面ABCD⊥平面PCD,平面ABCD∩平面PCD=CD,CD⊥PC,PC⊂平面PCD,
∴PC⊥平面ABCD,∵BD⊂平面ABCD,
∴BD⊥PC,
∵四边形ABCD是等腰梯形,AD=AB=BC=
| 1 |
| 2 |
则cos∠BCD=
| ||
| BC |
| 1 |
| 2 |
∴BD2=BC2+CD2-BC•CD=3BC2,∴BC2+BD2=CD2,
∴BD⊥BC,
又BC∩PC=C,BC⊂平面PBC,PC⊂平面PBC,
∴BD⊥平面PBC,又BD⊂平面PBD,
∴平面PBD⊥平面PBC.
看了 如图,三角形PCD所在的平面...的网友还看了以下:
如图,在直角三角形ABC中,角C=90度,AC=12,BC=5.在直角三角形ABC的外部拼凑一个合 2020-05-17 …
如图所示,一个长方形恰好分成六个小正方形有一个长方形如图所示,恰好分成六个正方形,其中最小的正方形 2020-06-02 …
(2011•上海)两波源S1、S2在水槽中形成的波形如图所示,其中实线表示波峰,虚线表示波谷,则( 2020-06-22 …
如图①,边长为a的大正方形中有一个边长为b的小正方形.如图所示,边长为a的大正方形中有一个边长为b 2020-07-13 …
一列简谐横波在x轴上传播,某时刻的波形如图所示,a、b、c为三个质元,a正向上运动.由此可知()A 2020-07-31 …
原三角形如图所示,如图1,原三角形内部有1个点时,原三角形可被分成3个三角形;如图2,原三角形内部有 2020-11-11 …
如图所示,甲、乙两列完全相同的横波,分别从波源A、B两点沿直线x轴相向传播,已知在t=0时的波形如图 2020-12-15 …
已知2x的平方+2x-3=0,求代数式x(x的平方-x-1)+2(x的平方+1)-三分之一x(3x的 2020-12-17 …
一根单线从纽扣的4个孔中穿过(每个孔只穿过一次),其正面情形如图所示,下面4个图形可能是其背面情形的 2020-12-25 …
如图所示,两列简谐波沿x轴相向而行,波速均为v=0.5m/s,两波源分别位于A、B处,t=0时的波形 2021-01-12 …