已知椭圆C：的一个焦点与短轴的两个端为的连线互相垂直，椭圆上的点到焦点的最大距离（Ⅰ）求椭圆C的方程．（Ⅱ）过轴上一点（的直线交椭圆C于A，B两点，试问：在椭圆C上是

Question

已知椭圆C：的一个焦点与短轴的两个端为的连线互相垂直，椭圆上的点到焦点的最大距离

   （Ⅰ）求椭圆C的方程．

（Ⅱ）过轴上一点（的直线交椭圆C于A，B两点，试问：在椭圆C上是否存在定点T，使得无论直线如何转动，以AB为直径的圆恒过定点T?若存在，求出的值及点T的坐标，若不存在，请说明理由.

Answer 1

（Ⅰ）设椭圆C：的右焦点为

        依题目意得：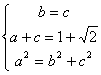             

        解得：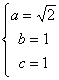                         

        所以，椭圆方程为：           

（Ⅱ）当直线的斜率不存在时，直线的方程为，

     由，得：          

     此时以为直径的圆的方程为：

    当：直线的斜率为0时，直线的方程为

    此时以为直径的圆的方程为：   

    要使定点存在，可知方程联立方程组只有一解，

                             

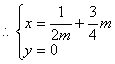
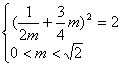解得                 

所以点的坐标为时，可能椭圆上存在定点满足题意.

当过点直线斜率存在时，存在定点满足题意，

设直线的方程为：，

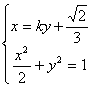由，得：   

            

此时，

                                                         

因些，过点直线斜率存在时，以为直径的圆过定点

综上所述：存在定点满足题意。