已知椭圆x2a2+y2b2=1（a>b>0）右顶为A，点P在椭圆上，O为坐标原点，且OP⊥PA，求椭圆的离心率e的取值范围．

Question

已知椭圆(x2)/(a2)+(y2)/(b2)=1（a>b>0）右顶为A，点P在椭圆上，O为坐标原点，且OP⊥PA，求椭圆的离心率e的取值范围．

Answer 1

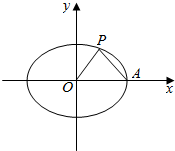∵∠AP0=90゜，∴点P在以AO为直径的圆上，
∵O（0，0），A（a，0），
∴以AO为直径的圆方程为x²+y²-ax=0，
联立

(x2)/(a2)+(y2)/(b2)=1

x2+y2-ax=0

消去y，得（b²-a²）x²+a³x-a²b²=0．
设P（m，n），则m+a=-(a3)/(b2-a2)，ma=(-a2b2)/(b2-a2)，可得m=(ab2)/(a2-b2)．
∵由图形得0<m<a，∴0<(ab2)/(a2-b2)<a，
即b²<a²-b²，可得a²-c²<c²，得a²<2c²，
∴e²>(1)/(2)，∴e>(√(2))/(2)．
又∵e∈（0，1），
∴椭圆的离心率e的取值范围为（(√(2))/(2)，1）．