早教吧作业答案频道 -->数学-->
如图,AB是O的直径,点C、D在O上,∠A=2∠BCD,点E在AB的延长线上,∠AED=∠ABC(1)求证:DE与O相切;(2)若BF=2,DF=10,求O的半径.
题目详情
如图,AB是 O的直径,点C、D在 O上,∠A=2∠BCD,点E在AB的延长线上,∠AED=∠ABC
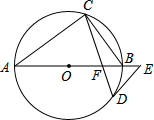
(1)求证:DE与 O相切;
(2)若BF=2,DF=
,求 O的半径.

(1)求证:DE与 O相切;
(2)若BF=2,DF=
| 10 |
▼优质解答
答案和解析
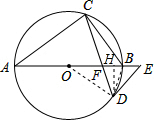 (1)证明:连接OD,
(1)证明:连接OD,
∵AB是 O的直径,
∴∠ACB=90°,
∴∠A+∠ABC=90°,
∵∠BOD=2∠BCD,∠A=2∠BCD,
∴∠BOD=∠A,
∵∠AED=∠ABC,
∴∠BOD+∠AED=90°,
∴∠ODE=90°,
即OD⊥DE,
∴DE与 O相切;
(2) 连接BD,过D作DH⊥BF于H,
∵DE与 O相切,
∴∠BDE=∠BCD,
∵∠AED=∠ABC,
∴∠AFC=∠DBF,
∵∠AFC=∠DFB,
∴△ACF与△FDB都是等腰三角形,
∴FH=BH=
BF=1,则FH=1,
∴HD=
=3,
在Rt△ODH中,OH2+DH2=OD2,
即(OD-1)2+32=OD2,
∴OD=5,
∴ O的半径是5.
 (1)证明:连接OD,
(1)证明:连接OD,∵AB是 O的直径,
∴∠ACB=90°,
∴∠A+∠ABC=90°,
∵∠BOD=2∠BCD,∠A=2∠BCD,
∴∠BOD=∠A,
∵∠AED=∠ABC,
∴∠BOD+∠AED=90°,
∴∠ODE=90°,
即OD⊥DE,
∴DE与 O相切;
(2) 连接BD,过D作DH⊥BF于H,
∵DE与 O相切,
∴∠BDE=∠BCD,
∵∠AED=∠ABC,
∴∠AFC=∠DBF,
∵∠AFC=∠DFB,
∴△ACF与△FDB都是等腰三角形,
∴FH=BH=
| 1 |
| 2 |
∴HD=
| DF2-FH2 |
在Rt△ODH中,OH2+DH2=OD2,
即(OD-1)2+32=OD2,
∴OD=5,
∴ O的半径是5.
看了 如图,AB是O的直径,点C、...的网友还看了以下:
高二不等式比较大小已知f(x)=(1+√(1+x))/x,a、b是两个不相等的实数,则下列不等式正 2020-04-26 …
已知,如图所示,点c为半圆o上的一点弧AC=弧CE,过点C作直径AB的垂线CP,垂足为P,弦AE分 2020-05-16 …
若(3x+1)^5=ax^5+bx^4+cx^3+dx^2+ex+f,求f的值 2020-05-16 …
(3x+1)∧5=ax∧5+bx^4+cx^3+dx∧2+ex+f,求a-b+c-d+e-f的值, 2020-05-16 …
这道高三函数题怎么做?函数f(x)的定义域为R,若f(x+1)与飞(x-1)都是奇函数,则A.f( 2020-05-20 …
已知函数y=f(x)是定义在R上的奇函数,且当x≥0时,f(x)=-2x则f(x)是()(A)f( 2020-07-12 …
已知a+b+c=0,a^-1+b^-1+c^-1=4,求a^-2+b^-2+c^-2的值还有一题设 2020-07-19 …
已知f(x)是定义(-00,+00)上的奇函数且f(x)在[0,+00)上是减函数,下列关系正确的 2020-08-01 …
已知(x+1)^6=a6x^6+a5x^5+a4x^4+a3x^3+a2x^2+a1x+a0当x=1 2020-10-31 …
若f(x)是R上的的偶函数且在0,+正无穷极)上是增函数,则下列成立的a.f(-2)大于f(0)大于 2020-12-08 …