早教吧作业答案频道 -->数学-->
已知圆C1:(x-4)2+(y-2)2=20与y轴交于O,A两点,圆C2过O,A两点,且直线C2O与圆C1相切;(1)求圆C2的方程;(2)若圆C2上一动点M,直线MO与圆C1的另一交点为N,在平面内是否存在定点P使得PM=PN始
题目详情
已知圆C1:(x-4)2+(y-2)2=20与y轴交于O,A两点,圆C2过O,A两点,且直线C2O与圆C1相切;
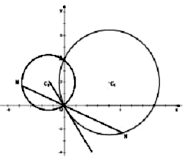
(1)求圆C2的方程;
(2)若圆C2上一动点M,直线MO与圆C1的另一交点为N,在平面内是否存在定点P使得PM=PN始终成立,若存在求出定点坐标,若不存在,说明理由.

(1)求圆C2的方程;
(2)若圆C2上一动点M,直线MO与圆C1的另一交点为N,在平面内是否存在定点P使得PM=PN始终成立,若存在求出定点坐标,若不存在,说明理由.
▼优质解答
答案和解析
(1)由(x-4)2+(y-2)2=20,令x=0,解得y=0或4.
∵圆C2过O,A两点,∴可设圆C2的圆心C1(a,2).
直线C2O的方程为:y=
x,即x-2y=0.
∵直线C2O与圆C1相切,∴
=
,解得a=-1,
∴圆C2的方程为:(x+1)2+(y-2)2=(
)2,化为:x2+y2+2x-4y=0.
(2)存在,且为P(3,4).
设直线OM的方程为:y=kx.
代入圆C2的方程可得:(1+k2)x2+(2-4k)x=0.
xM=
,yM=
.
代入圆C1的方程可得:(1+k2)x2-(8+4k)x=0.
xN=
,yN=
.
设P(x,y),线段MN的中点E(
,
).
则
×k=-1,
化为:k(4-y)+(3-x)=0,
令4-y=3-x=0,解得x=3,y=4.
∴P(3,4)与k无关系.
∴在平面内是存在定点P(3,4)使得PM=PN始终成立.
∵圆C2过O,A两点,∴可设圆C2的圆心C1(a,2).
直线C2O的方程为:y=
| 1 |
| 2 |
∵直线C2O与圆C1相切,∴
| |a-4| | ||
|
| a2+4 |
∴圆C2的方程为:(x+1)2+(y-2)2=(
| 5 |
(2)存在,且为P(3,4).
设直线OM的方程为:y=kx.
代入圆C2的方程可得:(1+k2)x2+(2-4k)x=0.
xM=
| 4k-2 |
| 1+k2 |
| 4k2-2k |
| 1+k2 |
代入圆C1的方程可得:(1+k2)x2-(8+4k)x=0.
xN=
| 8+4k |
| 1+k2 |
| 4k2+8k |
| 1+k2 |
设P(x,y),线段MN的中点E(
| 4k+3 |
| 1+k2 |
| 4k2+3k |
| 1+k2 |
则
| ||
|
化为:k(4-y)+(3-x)=0,
令4-y=3-x=0,解得x=3,y=4.
∴P(3,4)与k无关系.
∴在平面内是存在定点P(3,4)使得PM=PN始终成立.
看了 已知圆C1:(x-4)2+(...的网友还看了以下:
如图,E、F、G、H分别是空间四边形ABCD各边上的点,且有AE∶EB=AH∶HD=mCF∶FB= 2020-05-15 …
相似三角形的两道大题(过程)1,在长为8厘米,宽为6厘米的矩形中,截去一个矩形,若留下的矩形与原矩 2020-06-02 …
已知两个母线相等的圆锥的侧面展开图恰能拼成一个圆,且它们的侧面积之比为1:2,则它们的高之比为?给 2020-06-03 …
对于平面直角坐标系中任意两点M(x1,y1),N(x2,y2),称|x1-x2|+|y1-y2|为 2020-06-14 …
厄,初一呐数学题目,#·#1.若a=3,b=5,则a^2008+b^2008的末位数字是多少呐?- 2020-06-28 …
1.已知一个等腰三角形的两边是方程4-(x-10)平方=0的两根,求等腰三角形面积?2.已知关于x 2020-07-01 …
1.已知一个等腰三角形的两边是方程4-(x-10)平方=0的两根,求等腰三角形面积?2.已知关于x 2020-07-01 …
若m^2=m+1,n^2-n-1=0且m不等于n,求代数式m^7+n^7的值由m^2=m+1,得, 2020-07-31 …
如图,四棱锥S-ABCD中,ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2A 2020-11-02 …
已知关于x的方程4x^2–(m-1)x+m-7=01,当两根互为相反数时,求m的取值.2,当已知关于 2020-12-01 …