早教吧作业答案频道 -->数学-->
类比平面几何中的射影定理:若直角三角形ABC中(如图),AB、AC互相垂直,AD是BC边的高,则AB2=BD•BC;AC2=CD•BC.若在三棱锥A-BCD中(如图),三个侧面ABC、ACD、ADB两两互相垂直,O是点A在平
题目详情
类比平面几何中的射影定理:若直角三角形ABC中(如图),AB、AC互相垂直,AD是BC边的高,则AB2=BD•BC;AC2=CD•BC.若在三棱锥A-BCD中(如图),三个侧面ABC、ACD、ADB两两互相垂直,O是点A在平面BCD上的投影,则三棱锥的侧面面积与它在底面上的投影面积和底面积的之间满足的关系为___(只需填一个)


▼优质解答
答案和解析
结论:S△ABC2=S△DBC•S△BCD.
证明如下
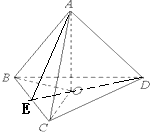 在△BCD内,延长DO交BC于E,连接AE,
在△BCD内,延长DO交BC于E,连接AE,
∵AD⊥平面ABC,BC⊂平面ABC,
∴BC⊥AD,
同理可得:BC⊥AO
∵AD、AO是平面AOD内的相交直线,
∴BC⊥平面AOD
∵AE、DE⊂平面AOD
∴AE⊥BC且DE⊥BC
∵△AED中,EA⊥AD,AO⊥DE
∴根据题中的已知结论,得AE2=EO•ED
两边都乘以(
BC)2,得(
BC•AE)2=(
BC•EO)•(
BC•ED)
∵AE、EO、ED分别是△ABC、△BCO、△BCD的边BC的高线
∴S△ABC=
BC•AE,S△BC0=
BC•EO,S△BCD=
BC•ED
∴有S△ABC2=S△DBC•S△BC0.
故答案为:S△ABC2=S△DBC•S△BCO.
证明如下
 在△BCD内,延长DO交BC于E,连接AE,
在△BCD内,延长DO交BC于E,连接AE,∵AD⊥平面ABC,BC⊂平面ABC,
∴BC⊥AD,
同理可得:BC⊥AO
∵AD、AO是平面AOD内的相交直线,
∴BC⊥平面AOD
∵AE、DE⊂平面AOD
∴AE⊥BC且DE⊥BC
∵△AED中,EA⊥AD,AO⊥DE
∴根据题中的已知结论,得AE2=EO•ED
两边都乘以(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AE、EO、ED分别是△ABC、△BCO、△BCD的边BC的高线
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴有S△ABC2=S△DBC•S△BC0.
故答案为:S△ABC2=S△DBC•S△BCO.
看了 类比平面几何中的射影定理:若...的网友还看了以下:
选择大小和生长情况相同的AB两碗豌豆豆苗,分别种在相同的培养液中,在相同食物生长条件下测量各自一天内 2020-03-31 …
选择大小和生长情况相同的AB两碗豌豆豆苗,分别种在相同的培养液中,在相同食物生长条件下测量各自一天内 2020-03-31 …
两个截面不同,长度相等的均匀铜棒接在电路中,两端的电压为U2.如图所示,两个截面不同,长度相等的均 2020-05-14 …
如图(1),在△ABC中,AB=AC,∠A=36°.(1)直接写出∠ABC的度数;(2)如图(2) 2020-06-02 …
甲、乙两人分别从AB两地同时出发,甲的速度是80米每分,乙的速度是60米每分,两人在途中的C点相遇 2020-06-04 …
已知空气的平均相对分子质量为29.在相同条件下,有一贮气瓶在空气中称重为179g,当充满氢气后称? 2020-07-03 …
有一块金属,在空中称得重3.8牛顿,将它浸没在盛满水的溢水杯中时,有50毫升的水从溢水杯中流入量筒 2020-07-05 …
若两种物质的稀水溶液在相同温度下渗透压相等,则下列说法中错误的是()若两种物质的稀水溶液在相同温度 2020-07-08 …
同位角、内错角、同旁内角在同一个“三线八角”的基本图形中,已知一对同位角相等.①在图中其余的各对同 2020-07-29 …
(1)在一个平面上画一组间距为d=4cm的平行线,将一根长度为l=3cm的针任意投掷在这个平面上, 2020-08-01 …