早教吧作业答案频道 -->数学-->
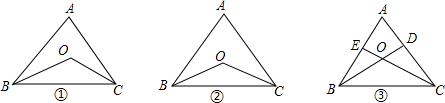
如图,在△ABC中,∠A=m°.(1)如图①,当O是△ABC的内心时,求∠BOC的度数;(2)如图②,当O是△ABC的外心时,求∠BOC的度数;(3)如图③,当O是高线BD与CE的交点时,求∠BOC的度数.
题目详情
如图,在△ABC中,∠A=m°.
(1)如图①,当O是△ABC的内心时,求∠BOC的度数;
(2)如图②,当O是△ABC的外心时,求∠BOC的度数;
(3)如图③,当O是高线BD与CE的交点时,求∠BOC的度数.
(1)如图①,当O是△ABC的内心时,求∠BOC的度数;
(2)如图②,当O是△ABC的外心时,求∠BOC的度数;
(3)如图③,当O是高线BD与CE的交点时,求∠BOC的度数.

▼优质解答
答案和解析
(1)∵O为△ABC的内心,
∴∠ABO=∠OBC=
ABC,∠ACO=∠OCB=
∠ACB,
∵∠ABC+∠ACB=180°-∠A=180°-m°,
∴
(∠ABC+∠ACB)=90°-
m°,
即∠OBC+∠OCB=90°-
m°,
∴∠BOC=180°-(∠OBC+∠OCB)=90°+
m°;
(2)∵点O为△ABC的外心,
∴由圆周角定理得:∠BOC=2∠A=2m°;
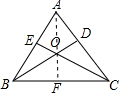
(3)连接AO,并延长与BC边相交于点F,则AF⊥BC,
∵BD⊥AC,CE⊥AB,
∴∠ABD=∠ACE=90°-∠BAC=90°-m°,
∴∠BOC=∠BOF+∠COF=∠BAF+∠ABD+∠CAF+∠ACE=∠ABD+∠BAC+∠ACE=2×(90°-m°)+m°=180°-m°.
∴∠ABO=∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ABC+∠ACB=180°-∠A=180°-m°,
∴
| 1 |
| 2 |
| 1 |
| 2 |
即∠OBC+∠OCB=90°-
| 1 |
| 2 |
∴∠BOC=180°-(∠OBC+∠OCB)=90°+
| 1 |
| 2 |
(2)∵点O为△ABC的外心,
∴由圆周角定理得:∠BOC=2∠A=2m°;

(3)连接AO,并延长与BC边相交于点F,则AF⊥BC,
∵BD⊥AC,CE⊥AB,
∴∠ABD=∠ACE=90°-∠BAC=90°-m°,
∴∠BOC=∠BOF+∠COF=∠BAF+∠ABD+∠CAF+∠ACE=∠ABD+∠BAC+∠ACE=2×(90°-m°)+m°=180°-m°.
看了 如图,在△ABC中,∠A=m...的网友还看了以下:
关于电场强度的定义式E=F/q,下列说法正确的是()A.q为负电荷时E的方向与q为正电荷时的方向相反 2020-03-30 …
在平行四边形ABCD中,点E,F分别是线段AD,BC上的两动点,点E从点A向D运动在平行四边形AB 2020-05-13 …
曲线Ⅰ和曲线Ⅱ(见右下图)代表物种1和物种2的耐热范围,在什么温度下物种2能竞争过物种1?A.温度 2020-05-14 …
在物理学内容中,如果某一物体质量为m,它运动时的能量E与它的运动速度v之间的关系(1)若物体质量为 2020-05-16 …
根据经度相差15度,时间即相差1小时计算,A,B两地的时间相差_____小时A(40度N,70度W 2020-05-17 …
一个等效平衡题某温度下密闭容器中发生如下可逆反应2E[g]==F[g]+xG[g]若起始时E的浓度 2020-06-06 …
如图①,梯形ABCD中,∠C=90°.动点E、F同时从点B出发,点E沿折线BA-AD-DC运动到点 2020-06-12 …
如图,在△ABC中,AD平分∠BAC,P为线段AD上一个动点,PE⊥AD交直线BC于点E①若∠B= 2020-06-27 …
路程、速度、时间三者之间的乘法数量关系式是,三者之间的除法数量关系式有A.路程×时间=速度B.路程 2020-06-27 …
当x→0时e^x是x^n的高阶无穷小吗?x→+∞e^x的增长速度比x^n当x→0时e^x是x^n的 2020-07-01 …