以Rt△ABC的两条直角边AB、BC为边，在三角形ABC的外部作等边三角形ABE和等边三角形BCF，EA和FC的延长线相交于点M，则点B一定是三角形EMF的（）A.垂心B.重心C.内心D.外心

Question

以Rt△ABC的两条直角边AB、BC为边，在三角形ABC的外部作等边三角形ABE和等边三角形BCF，EA和FC的延长线相交于点M，则点B一定是三角形EMF的（　　）

A. 垂心

B. 重心

C. 内心

D. 外心

Answer 1

如图，

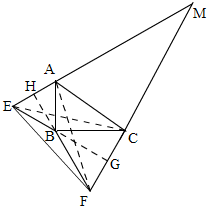
连接CE，AF，延长EB交MF于G，延长FB交ME于H，
∵以Rt△ABC的两条直角边AB，BC为边作等边△ABE和等边△BCF，
∴∠CBE=90°+60°=150°，∠FBE=360°-90°-60°-60°=150°，
在△CBE与△FBE中，

CB=BF

∠CBE=∠FBE

BE=BE

，
∴△CBE≌△FBE（SAS）；
∴CE=FE，∠FEB=∠CEB，
∴BE⊥CF于G，
∴EG是△MEF的边FM上的高，
同理：FH是△MEF的边EM上的高，
∴点B是△MEF的三边的高，
即：点B是△MEF的垂心．
故选A．