早教吧作业答案频道 -->数学-->
已知,在菱形ABCD中,∠ADC=60°,点F为CD上任意一点(不与C、D重合),过点F作CD的垂线,交BD于点E,连接AE.(1)①依题意补全图1;②线段EF、CF、AE之间的等量关系是.(2)在图1中将
题目详情
已知,在菱形ABCD中,∠ADC=60°,点F为CD上任意一点(不与C、D重合),过点F作CD的垂线,交BD于点E,连接AE.
(1)①依题意补全图1;
②线段EF、CF、AE之间的等量关系是___.
(2)在图1中将△DEF绕点D逆时针旋转,当点F、E、C在一条直线上(如图2).线段EF、CE、AE之间的等量关系是___.写出判断线段EF、CE、AE之间的等量关系的思路(可以不写出证明过程)
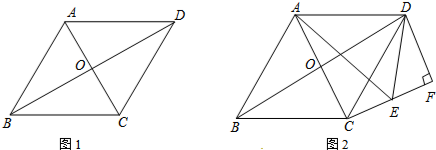
(1)①依题意补全图1;
②线段EF、CF、AE之间的等量关系是___.
(2)在图1中将△DEF绕点D逆时针旋转,当点F、E、C在一条直线上(如图2).线段EF、CE、AE之间的等量关系是___.写出判断线段EF、CE、AE之间的等量关系的思路(可以不写出证明过程)

▼优质解答
答案和解析
解(1)①依题意补全图形如图1所示,
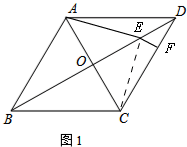
②连接CE,
∵四边形ABCD为菱形,
∴BD⊥AC,BD平分AC,
∴AE=CE,
∵EF⊥CD,
∴∠EFC=90°,
根据勾股定理得,CE2=EF2+CF2,
∴AE2=EF2+CF2,
故答案为AE2=EF2+CF2;
(2)如图2,
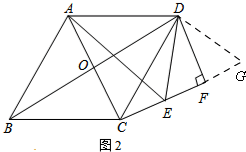
延长EF至G,使EF=FG,连接DG,
∴EG=2EF,
∵DF⊥CF,
∴DE=DG,∠EDG=2∠EDF
∵四边形ABCD是菱形,
∴AD=CD,∠ADC=2∠0DC=60°,
由旋转得,∠ODC=∠EDF,
∴∠ADC=∠EDG,
∴∠ADE=∠CDG,
在△ADE和△CDG中
∵
,
∴△ADE≌△CDG,
∴AE=CG=CE+EG=CE+2EF,
∴AE=CE+2EF,
故答案为AE=CE+2EF.

②连接CE,
∵四边形ABCD为菱形,
∴BD⊥AC,BD平分AC,
∴AE=CE,
∵EF⊥CD,
∴∠EFC=90°,
根据勾股定理得,CE2=EF2+CF2,
∴AE2=EF2+CF2,
故答案为AE2=EF2+CF2;
(2)如图2,

延长EF至G,使EF=FG,连接DG,
∴EG=2EF,
∵DF⊥CF,
∴DE=DG,∠EDG=2∠EDF
∵四边形ABCD是菱形,
∴AD=CD,∠ADC=2∠0DC=60°,
由旋转得,∠ODC=∠EDF,
∴∠ADC=∠EDG,
∴∠ADE=∠CDG,
在△ADE和△CDG中
∵
|
∴△ADE≌△CDG,
∴AE=CG=CE+EG=CE+2EF,
∴AE=CE+2EF,
故答案为AE=CE+2EF.
看了 已知,在菱形ABCD中,∠A...的网友还看了以下:
关于E=Fq和E=KQr2两个公式,下列说法中正确的是()A.E=Fq中的场强E是电荷q产生的B. 2020-05-13 …
图中E、F、G、H代表生物体内的有机大分子,A、B、C、D代表组成它们的基本单位,请据图回答相关问 2020-05-13 …
如图,在菱形ABCD中,∠A=60°,AD=8,F是AB的中点.过点F作FE⊥AD,垂足为E.将△ 2020-06-15 …
已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E 2020-07-09 …
(2213•永州k模)如图的几何体中,AB⊥平面AC少,少E⊥平面AC少,△AC少为等边三角形,A少 2020-11-02 …
如图表示的是细胞中含有的四种有机物的结构与功能.请据图回答:(1)图中E含有的元素有,A是.(2)图 2020-11-08 …
读世界轮廓图回答下列问题:(1)在图中适当的位置标注对应的符号:A.(45°N,15°E);B.(3 2020-11-11 …
读世界轮廓图回答下列问题:(1)在图中适当的位置标注对应的符号:A.(45°N,15°E);B.(3 2020-11-11 …
(2012•宜宾)已知A、B、C、D、E、F、G、H、I均为初中化学常见的物质.其中E、G为常见金属 2020-11-12 …
A.《本草纲目》a.吴承恩B.《天工开物》b.李时珍C.《三国演义》c.施耐庵D.《水浒传》d.罗 2020-11-23 …