早教吧作业答案频道 -->数学-->
如图,菱形ABCD,以A为圆心,AC长为半径的圆分别交边BC,DC,AB,AD于点E,F,G,H.(1)求证:CE=CF;(2)当E为弧CG中点时,求证:BE2=CE•CB.
题目详情
如图,菱形ABCD,以A为圆心,AC长为半径的圆分别交边BC,DC,AB,AD于点E,F,G,H.
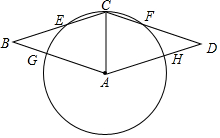
(1)求证:CE=CF;
(2)当E为弧
中点时,求证:BE2=CE•CB.

(1)求证:CE=CF;
(2)当E为弧
 |
| CG |
▼优质解答
答案和解析
(1)证明:连接AE,AF,
∵四边形ABCD是菱形,
∴∠ACB=∠ACF,
∵AE=AC=AF,
∴∠AEC=∠ACE=∠ACF=∠AFC,
∴∠EAC=180°-∠AEC-∠ACE,
∠CAF=180°-∠ACF-∠AFC,
∴∠EAC=∠FAC,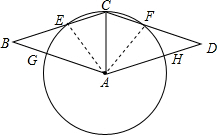
∴
=
,
∴CE=CF;
(2) ∵E为弧
中点,
∴∠CAE=∠BAE,
∵AB=BC,AE=AC,
∴∠ACE=∠AEC=∠BAC=∠B+∠BAE,
∴∠B=∠BAE,
∴BE=AE=AC,
∴△ABC∽△CAE,
∴
=
,
∴AC2=BC•CE,
即BE2=CE•CB.
∵四边形ABCD是菱形,
∴∠ACB=∠ACF,
∵AE=AC=AF,
∴∠AEC=∠ACE=∠ACF=∠AFC,
∴∠EAC=180°-∠AEC-∠ACE,
∠CAF=180°-∠ACF-∠AFC,
∴∠EAC=∠FAC,

∴
 |
| CE |
 |
| CF |
∴CE=CF;
(2) ∵E为弧
 |
| CG |
∴∠CAE=∠BAE,
∵AB=BC,AE=AC,
∴∠ACE=∠AEC=∠BAC=∠B+∠BAE,
∴∠B=∠BAE,
∴BE=AE=AC,
∴△ABC∽△CAE,
∴
| AC |
| BC |
| CE |
| AC |
∴AC2=BC•CE,
即BE2=CE•CB.
看了 如图,菱形ABCD,以A为圆...的网友还看了以下:
已知函数f(X)=x^(-1/2p^2+p+3/2)(p属于Z)在(0,+无穷)上是增函数,且在其 2020-05-13 …
在△ABC中,边AB,BC的垂直平分线交于点P. 1.求证PA=PB=PC. 2.点P是否也在边A 2020-05-16 …
在面积为1的三角形ABC 中,P为边 BC的中点,点 Q在边AC 上,且AQ=2QC ,连接AP 2020-05-16 …
将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC 2020-05-17 …
求不等式a^3x-7>a^5x-1(a>0且a不等于1)中实数x的取值范围 2020-06-02 …
有位同学发现了“角平分线”的另一种尺规作法,其方法为:1以O为圆心,任意长为半径画弧分别交OM,O 2020-06-06 …
关于初中一数学题!在1×1的正方形网格中只有一个边长为1的正方形;在2×2的正方形网格中有1个边长 2020-07-04 …
x从左边趋于1,即x小于1趋于1,x/(1-x)=?是正无穷还是负无穷?x从右边趋于1,即x大于趋 2020-07-18 …
如图1,正方形ABCD和正方形QMNP,M是正方形ABCD的对称中心,边MN与边AB交于F,边AD 2020-07-22 …
课本上有一个例题:1+3+5+...+(2n-1)=n²,当n=1时,左边=1,想问下为什么等于1 2020-08-01 …